Application / Solutions

Motor Design
Axial Gap Type Motor

Wound Field Synchronous Motor
Induction Heating
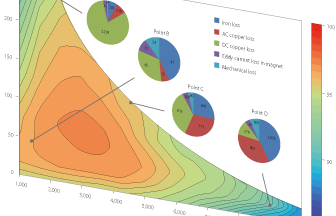
Model-Based Development
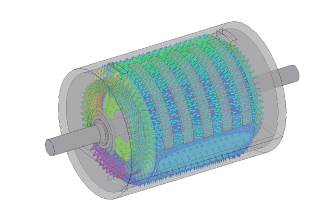
Thermal Analysis for Motor Design in JMAG

Utilizing JMAG in Cloud Services
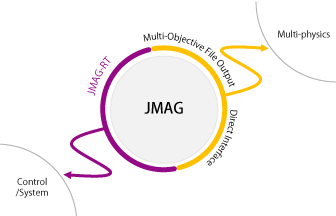
JMAG Open Interface programs
Case studies by users and applications for JMAG open interface programs are also available on this page. Upd