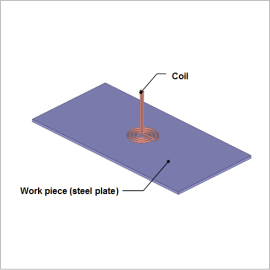
Overview

High-frequency induction heating is one heating method used when heat treating the surface of a steel plate. With induction heating, the heating depth can be adjusted because it is possible to localize heating by modifying the coil’s geometry and electrical power. The coil geometry, heating conditions, etc. must be designed correctly in order to achieve heating as desired, but the cost and time needed for prototyping can be a problem.
To make accurate predictions, it is necessary to account for the temperature dependency of the thermal conductivity, the electrical conductivity, and the detailed coil geometry in order to find the heat generation distribution. Electromagnetic field simulation using the finite element method (FEM) is needed for this type of prediction.
This Application Note presents how to confirm the uniformity of the surface temperature distribution in the steel plate facing the coil and check for an eddy current loss density distribution that causes the temperature distribution to be uneven, when a mosquito-coil-shaped coil is in position.

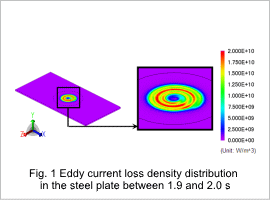
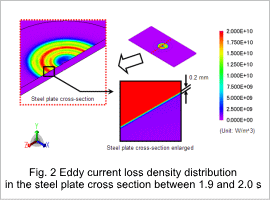
Eddy Current Loss Density Distribution

The eddy current loss density distribution generated in the steel plate and the eddy current loss density distribution in a cross-section of the steel plate are shown in Fig .1 and Fig .2.
The eddy currents generated by the magnetic field variations created by the coil are distributed to the surface of the steel plate by the skin effect.

Temperature Distribution

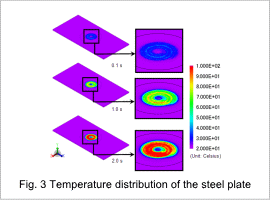
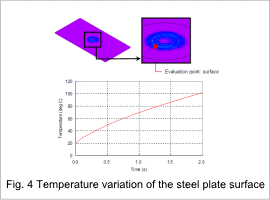
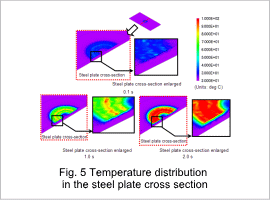
The temperature distribution of the steel plate at 0.1 s, 1.0 s, and 2.0 s is indicated in fig. 3. The temperature versus time is indicated in fig. 4, and the temperature distribution in the cross-section of the steel plate is indicated in fig. 5. The temperature of the surface of the steel plate rises over time, reaching about 100 deg C in the steel plate surface below the coil at 2.0 s. Heating occurs first in the surface, with the heat then transferred gradually to the inside of the steel plate, because the eddy currents are concentrated on the steel plate surface.
The temperature distribution of the steel plate is uneven because of the coil’s geometry. Improvements need to be made to the coil geometry in order to achieve uniform temperatures in the steel plate.