Overview

There are high hopes for SR motors to provide robustness and low cost, thanks to their relatively simple construction without permanent magnets. However, the large electromagnetic force produced by the saliency of their stator and rotor causes vibration and noise.
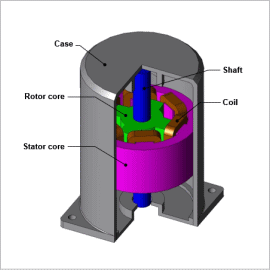
The electromagnetic force working in an SR motor causes vibration and noise as an electromagnetic excitation force. Vibration and noise are caused when this electromagnetic excitation force resonates with the motor’s eigenmode. In order to evaluate this phenomenon with acceptable precision, it is necessary to accurately ascertain the distribution of the electromagnetic force acting on the stator core, which is the source of radiated sound, and to obtain the eigenmode of the entire motor including its connected case.
In this example, how to obtain the electromagnetic force generated in the stator core of an SR motor and evaluate the sound pressure by linking it to the motor’s eigenmode.

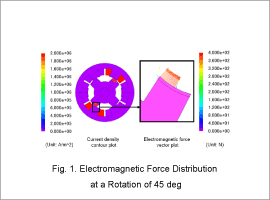
Current Density Distribution and Electromagnetic Force Distribution

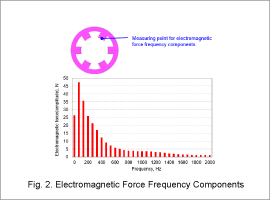
The contour plot of the current density distribution when the SR motor is at 45 deg of rotation and the vector plot of the electromagnetic force distribution of the stator core are indicated in Fig. 1. The frequency components of the electromagnetic force produced at the ends of the stator core’s teeth are indicated in Fig. 2.
The electromagnetic force at the stator core teeth tips gets very large from the timing of the current flow, as seen in Fig. 1. Fig. 2 shows that the 66.67 Hz frequency component is dominant in the electromagnetic force.

Eigenmode

The eigenmode at around 2,100 Hz is shown in Fig. 3. It can be seen that there is a mode at which the stator core is deformed to an ellipse at around 2,100 Hz. A great deal of vibration is likely to be caused by resonance phenomena between this eigenmode and the electromagnetic force.

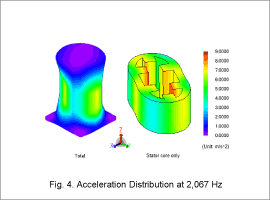
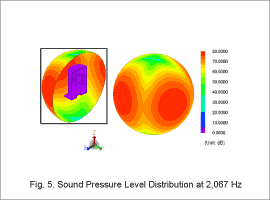
Acceleration Distribution and Sound Pressure Distribution

Fig. 4 shows the acceleration distribution at 2,067 Hz, the frequency at which the mode occurs with elliptical deformation confirmed by eigenmode analysis. Fig. 5 shows the sound pressure level distribution. It can be seen that at 2,067 Hz, electromagnetic resonance occurs between the electromagnetic force and the eigenmode shown in Fig. 3.