Overview
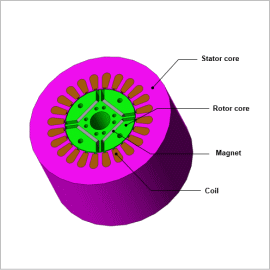
Although it is difficult to understand the temperatures of each part in a real machine, the temperatures of each of these parts can be obtained with ease through simulations, and changes to characteristics due to increases in temperature can also be taken into account. As methods of analysis that account for the increases in temperature for each part, there exists the method of coupled analysis between magnetic field analysis and thermal analysis, as well as the method of running magnetic field analysis that uses thermal equivalent circuits. Detailed evaluations that obtain temperature distribution are possible for coupled analysis. While the evaluation of temperature distribution is not possible when using thermal equivalent circuits, magnetic field analysis that accounts for temperature increases can be performed at high speeds with ease.
In this example, magnetic field analysis is run using a thermal equivalent circuit, and changes in average torque due to magnet demagnetization are checked.
Thermal Equivalent Circuit
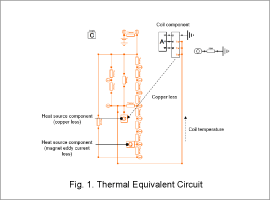
Loss is expressed by heat source components. Heat sources are copper loss and the eddy current loss of magnets.
Coil temperature calculated with the thermal equivalent circuit is fed back into Coil Component. Coil component retain temperature dependency in resistance values, and copper loss values are updated. The feedback of coil temperature and updates to copper loss are repeated, and part temperatures during thermal equilibrium are obtained.
Magnets demagnetize due to heat generation from eddy current loss, in addition to heat transmitted from the coils through parts and air gaps.
Part Temperature, Copper Loss
The thermal equivalent circuit during thermal equilibrium and the heat flow vectors of each component are shown in Fig. 2.
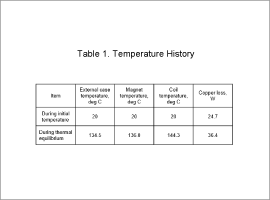
The coil temperature, magnet temperature, external case temperature, and copper loss during initial temperature and during thermal equilibrium are shown in Table 1.
From Fig. 2 it is understood that heat is transferred from the magnet to the external case via the rotor core and the shaft, then dissipated to the ambient air. The magnet and heat dissipation path temperatures are as per Table 1; the ambient air is 20 deg C, the external case temperature is 134.5 deg C, and the magnet temperature is 136.1 deg C. Because the difference in temperature between the external case and the magnet is small, it can therefore be determined that the cause of the rise in temperature for the magnet is mainly the small heat dissipation that occurs from the external case to the ambient air.
It is understood from Table 1 that copper loss also increases in accordance with the rise in coil temperature. In this analysis there are no changes in current due to temperature because drive occurs with a specified current. Specifically, the temperature increases the coil electric resistance and copper loss.

Average Torque
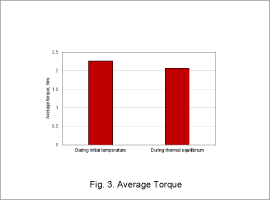
It is understood that average torque decreases during thermal equilibrium. As mentioned previously, there are no changes in current due to temperature. It can therefore be determined that the decrease in average torque is due to the thermal demagnetization of the magnets.


