Overview

Chopper inductors used in DC-DC converters suppress ripple currents caused by switching elements and provide stable DC voltage. With the trend toward miniaturization for easier integration into electric vehicles, the resonant frequency tends to decrease, while operating frequency increases due to high-frequency switching. These are conflicting requirements in terms of the increase in the operating range.
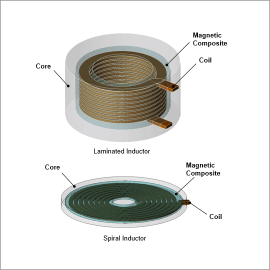
Electromagnetic field analysis is effective for designing chopper inductors, especially in high-frequency regions where displacement currents (capacitance) must be considered to understand resonance phenomena.
This case study explains modeling for frequency characteristics of impedance and loss using laminated and spiral-type chopper inductors.

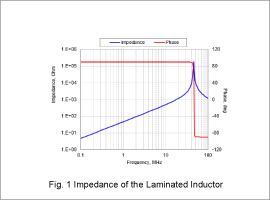
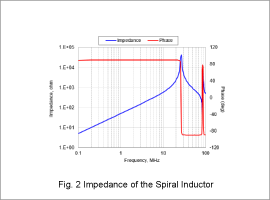
Impedance

The impedance of the laminated inductor is shown in Fig. 1, and that of the spiral inductor is shown in Fig. 2. It can be observed that the laminated inductor resonates at 46 MHz, while the spiral inductor resonates at 27 MHz.

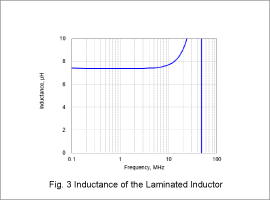
Inductance

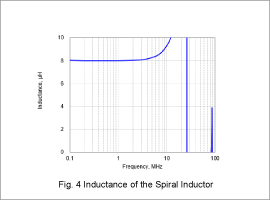
The inductance of the laminated inductor is shown in Fig. 3, and that of the spiral inductor is shown in Fig. 4. For the laminated inductor, the inductance remains stable at approximately 7.4 µH within the frequency range up to around 5 MHz. Similarly, for the spiral inductor, the inductance remains stable at approximately 8.0 µH within the frequency range up to around 3 MHz.

Q factor

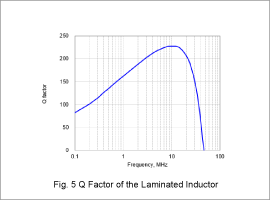
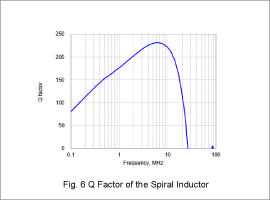
The Q factor of the laminated inductor is shown in Fig. 5, and that of the spiral inductor is shown in Fig. 6. The maximum Q factor reaches 228 around 10 MHz for the laminated inductor, and 231 around 5 MHz for the spiral inductor.

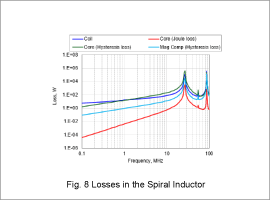
Loss

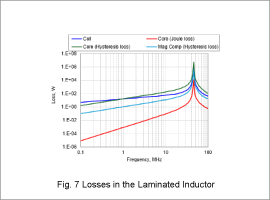
Fig. 7 shows the loss values of each component in the laminated inductor, and Fig. 8 shows those of the spiral inductor. In both structures – the laminated and spiral inductors a gradual increase in loss with rising frequency is observed. Notably, a sharp increase in loss occurs near the resonance frequency.

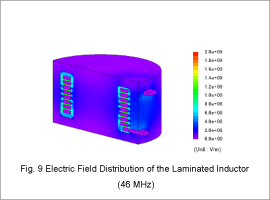
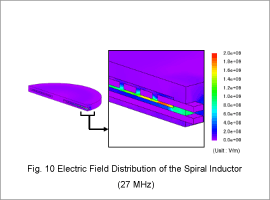
Electric Field Distribution

Fig. 9 shows the electric field distribution of the laminated inductor at the resonance frequency, and Fig. 10 shows that of the spiral inductor. In both structures the laminated and spiral inductors it can be observed that high electric field intensity is concentrated between the core and the conductor, as well as between conductors.

Computational Cost

In this case study, the analysis was conducted using a computing system equipped with two AMD EPYC 9684X processors (96 cores each) and 2,304 GB of memory.
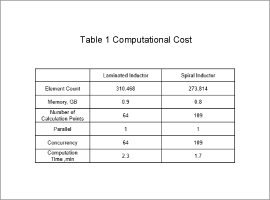
The computational cost is presented in Table 1.