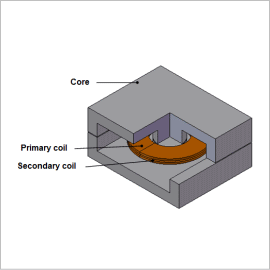
Power transformer requires large currents, so their geometry tends to be large. This means that they are particularly hard parts to miniaturize when electrical product designs get smaller. The sheet coil transformer introduced in this Application Note achieves thinner dimensions by winding its coil in a thin sheet.
Self-inductance and leakage inductance are critical items in a transformer’s design requirements. The amount of inductance is dependent on the magnetic circuit, but the nonlinear characteristics of the magnetic properties make it so that the magnetic circuit changes when the operating point changes. The leakage inductance has all of the same properties, but it also has a flux path in non-magnetic regions, making it easily affected by the geometry and coil arrangement in addition to the core. This is why a magnetic field analysis using the finite element method (FEM) is necessary when evaluating these types of inductance.
This Application Note explains how to obtain the self-inductance and leakage inductance of a sheet coil transformer.

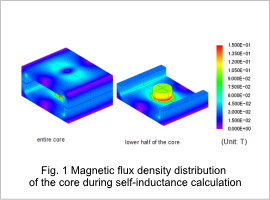
The magnetic flux density distribution used to calculate the self-inductance is indicated in fig. 1. The magnetic flux is concentrated at the center of the core, as indicated in the figure. The magnetic flux produced by the current flowing through the coil is split in two from the center core because the magnetic flux flows around the outer circumference of the core and then back to the center of the core.
The magnetic flux density is larger at the corners inside of the core than the outside of the core. This is because the magnetic flux flows through the shortest route of the core.

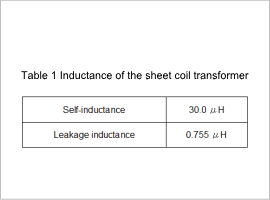
The inductance of the sheet coil transformer is indicated in table 1. The inductance can be obtained from the relationship between the voltage and current. The self-inductance is 30.0 μH, and the leakage inductance is 0.755 μH.