*Please prepare a license ID and password for the license administrator.
*It is different from the service for JMAG WEB MEMBER (free membership). Please be careful.
Overview
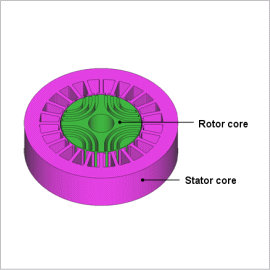
Skyrocketing prices of rare earth magnets have led to rising expectations for synchronous reluctance motors (referred to below as SynRMs), which do not use permanent magnets. SynRMs have a simple structure that can achieve solid performance at a low price. However, torque is generated only by the rotor’s saliency and the coil’s magnetomotive force, so raising the torque density depends greatly on the core’s nonlinear magnetic properties and the rotor geometry. This is why they have a different format than a typical motor. On the other hand, the aforementioned rising prices of rare earth magnets, improvements in current control technology, and the ability of optimization designs using magnetic field analysis have raised the possibility of lowering these barriers, giving SynRMs the chance to be reexamined.
SynRMs operate using the nonlinear region of a magnetic steel sheet, so the inductance expresses nonlinear behavior as well. This behavior distorts the excitation current waveform a great deal, making it impossible to run advanced projections that are accurate with calculation methods that follow linear formulas. Consequently, it becomes necessary to use the finite element method (FEM), which can handle nonlinear magnetic properties in material, detailed motor geometry, and transient currents.
This Application Note presents an evaluation of torque variations that occur when the phase of a sinusoidal wave current is changed.
SynRMs operate using the nonlinear region of a magnetic steel sheet, so the inductance expresses nonlinear behavior as well. This behavior distorts the excitation current waveform a great deal, making it impossible to run advanced projections that are accurate with calculation methods that follow linear formulas. Consequently, it becomes necessary to use the finite element method (FEM), which can handle nonlinear magnetic properties in material, detailed motor geometry, and transient currents.
This Application Note presents an evaluation of torque variations that occur when the phase of a sinusoidal wave current is changed.
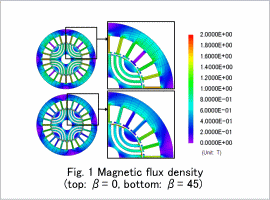
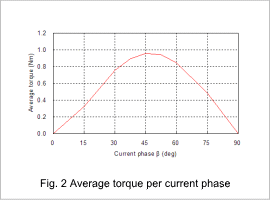
Magnetic Flux Density Distribution and Average Torque per Current Phase
The magnetic flux density distribution at a rotation speed of 600 r/min and a current amplitude of 3.0 A is shown in fig. 1. The average torque at each current phase is shown in fig. 2. The magnetic flux density distribution changes with the current phase. When the current phase is 0 deg and 90 deg the average torque is 0, and when the current phase is 45 deg the torque reaches its peak.