The finite-element method is very rarely exactly correct. Now surely that is an outrageous thing to say on the JMAG website! But what do we mean by exactly? The finite-element method begins with discretization : dividing the solution domain into a large number of small elements (triangles, rectangles, etc.) so that the continuous partial differential equations of the physics can be replaced by a large number of simultaneous algebraic equations. The solution of these is, of course, the natural job of the computer. But computers work with binary integers, and when the algebraic equations are nonlinear the question of convergence arises as well. So we are really and truly in a sophisticated world of successive approximation.
Discretization is itself an approximation : replacing continuous curves and surfaces with straight lines and plane facets. This is a source of inexactness. But if the mesh of discrete elements is sufficiently fine, the error can be made very small : so small, in fact, that we tend to accept the results of a finite-element calculation without question as though they were exact.
In classical analysis it might seem that the question of discretization error does not arise. However, classical analysis is generally capable of solving only idealized problems with relatively simple geometry. Although the mathematics could be sophisticated, it was common to make gross assumptions about the physics : for example, using 2D theory and ignoring end-effects in finite-length devices like electric machines. In the past it was never possible to analyse real structures and devices exactly, and in classical analysis there is no equivalent of mesh refinement to reduce the discretization errors systematically. In classical analysis, therefore, the errors (departures from reality) were essentially imponderable, and physical testing was necessary to evaluate them. In modern numerical analysis, mesh refinement is to a large extent automatic, and we often take it for granted.
When it comes to numerical evaluation, both classical analysis and numerical methods are limited by the precision of the computer. A slide-rule (fondly remembered) is an example of 3-decimal-digit precision (roughly equivalent to 9-bit binary precision); but now we are accustomed to 64-bit personal computers with huge ‘word-lengths’, so numerical precision is often taken for granted.
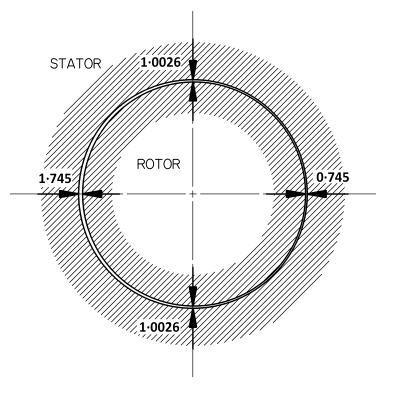
But what about the physical precision or exactness of the device we are analysing? We often see powerful numerical analysis tools being used to calculate idealized models of real devices. A simple example is the rotor/stator of an electric machine represented in the diagram. Isn’t it true that we normally expect the rotor and the stator bore to be round and concentric? Yet in reality they are often imperfect. The diagram shows a case where the rotor is ovalised by about 0.5%, and offset from the centre-line so that the airgap on one side is 2.3 times bigger than it is on the other side. If we measure the airgap at four places, we get three different results. On the factory floor, these measurements would be disturbing. What is the true shape of the rotor, and the stator? What is the shape of the all-important airgap as a function of the peripheral angle? And what are the effects of these departures from the ideal?
This last question, the most important question, could never be answered precisely by classical analysis. Some brave attempts have been made, of course : but (with no lack of respect to the great analytical engineers who went before us) the chance of a really precise answer was always low, and the chance of an exact answer was always zero. It is glaringly obvious that modern numerical analysis methods give us the facility to analyse imperfections, which we did not have before. Why don’t we do it more often?
Let’s do more. Let’s make a fuss about imperfections. Let’s incorporate the imperfect into our daily thinking about analytical design.