Contents
1. Introduction
2. Iterative Calculation and Convergence Tolerances
3. Point of View about Convergence Tolerances in Nonlinear Iteration
4. Point of View About Convergence Tolerance in the ICCG Method
5. Summary
6. References

1. Introduction

In electromagnetic field finite element analysis (FEA) which is often used in electrical equipment design, there are two iterative processes shown in Fig. 1. The outer loop is nonlinear iteration (Newton-Raphson) for deciding the material property, and the inner one is solving of linearized equations (ICCG). In these iterative processes, there are issues in which necessary precision cannot be obtained and/or unnecessary processing time is required unless the appropriate determination methods or tolerance values are used. To overcome these challenges, we are taking on various approaches to stabilize iterative processing.
In this report, we will explain the convergence criteria of a local quantity and the improvement of the determination of convergence of ICCG. And then, we describe that these ideas make a good effect to the known problems about the convergence characteristics.

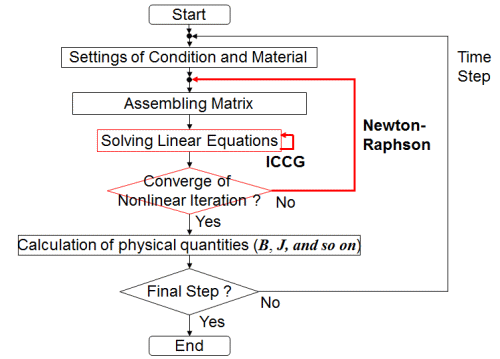
Fig. 1 Typical workflow for electromagnetic FEA.
There are two iterative calculation: Nonlinear and ICCG calculation in electromagnetic FEA.

2. Iterative Calculation and Convergence Tolerances

In the electromagnetic FEA, magnetic flux density fluctuates during the process of nonlinear iteration as shown in Fig. 2. When the fluctuation becomes less than the convergence criterion εNR, the magnetic flux density is considered to have converged. Moreover, the residuals that determine the convergence of the ICCG solution are closely related to the residuals of the nonlinear iterations [5]. The residual history of the ICCG solution at the 2nd time-step of an existing analysis is shown in Fig. 3. Since the residual of the ICCG solution (which is the vertical axis) is the value obtained by dividing by the magnitude of the residual of the first nonlinear iteration, a relationship between nonlinear and ICCG residuals can be seen. By paying attention to residuals in nonlinear iteration times, ICCG iterations may be performed so that it becomes sufficiently, and efficiently, small.

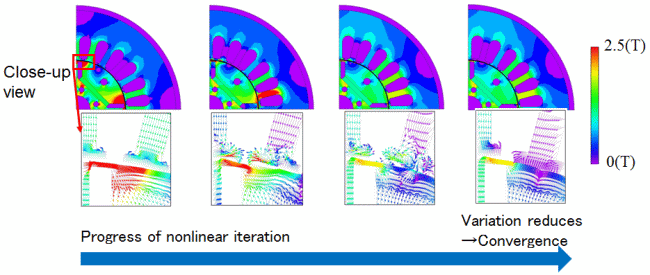
Fig. 2 Variation of magnetic flux density as the nonlinear iteration progresses.
As the nonlinear calculation progresses, fluctuation in the whole field decreases.

3. Point of View about Convergence Tolerances in Nonlinear Iteration

A method having the variation amount of the vector potential of each node (the edge in 3D analysis) as a parameter, such as in the following expression, is often used for nonlinear convergence determination methods.