Overview

Evaluating the inductance characteristics along the d/q-axis is important when analyzing the saliency of a rotor in an IPM motor. With actual measurements, it is possible to calculate the inductance in the d-axis and q-axis by measuring the no-load magnetic flux or the voltage and current with a three-phase current flowing when the motor is in actual operation. If it cannot be measured while the motor is operating, an LCR meter can be entered in two phases when the rotor is in a stationary state. However, current conditions are different between three phases and two phases, so the motor will express different characteristics during actual drive, especially when it is strongly affected by magnetic saturation. For this reason, the analysis contents need to be determined according to the situation of the actual measurements when comparing the measurements with an analysis.
This Application Note presents an analysis that obtains d/q-axis inductance in an IPM motor while assuming actual measurements in a stationary rotor.

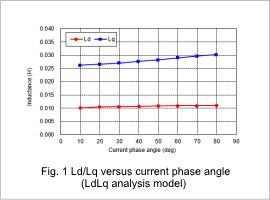
Ld/Lq versus current phase angle /Inductance

From fig. 1, it is apparent that the d-axis inductance hardly changes depending on the current phase angle. The reason for this is that the inductance is small because the d-axis magnetic flux passes through a magnet with low permeability, meaning that it is not very affected by the magnetic saturation of the iron core because the magnet’s magnetic resistance makes a big contribution. On the other hand, the magnetic flux from the q-axis passes through the iron core, so the permeability is large compared with the d-axis, meaning that the inductance is large as well. The current phase also progresses, so when the magnetic flux is weaker the iron core’s magnetic saturation is alleviated, meaning that the q-axis inductance increases.
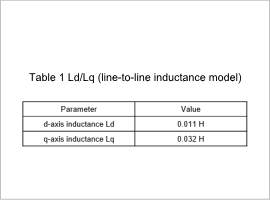
However, a three-phase current is not run with the method of calculation using the line-to-line inductance, so it is not possible to obtain the variations in d-axis/q-axis inductance caused by the current phase angle. The magnetic saturation conditions of the iron core are also different when running a three-phase AC and a line-to-line current, so the q-axis inductance has been generally overestimated. In contrast, the contribution of the aforementioned magnet’s magnetic resistance to the d-axis inductance is large, so there is not a big gap between the results of the two methods.