Overview
In this example, the acceleration is evaluated by obtaining the electromagnetic force generated in the stator core of the SPM motor at multiple rotation speeds and coupling with the eigenmodes of the motor. In addition, the frequency components of the electromagnetic force and eigenmodes and the spatial modes are analyzed, and the resonance modes are confirmed.
Eigenmodes
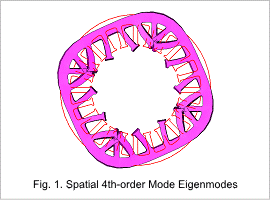
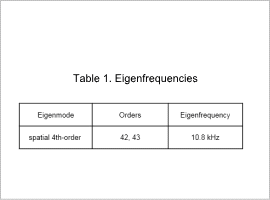
Notice the spatial 4th-order mode is focused on. From the eigenmode analysis results, the eigenfrequency for each vibration mode is found.
The spatial 4th-order mode results are shown in Fig. 1 and Table 1.
Rotation Speed, Frequency, and Acceleration Graphs
Coupled analysis of magnetic field transient response analysis and structural frequency response analysis is performed to evaluate the acceleration of the vibration excited by the electromagnetic force generated in the stator.
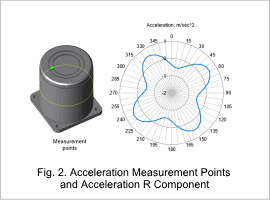
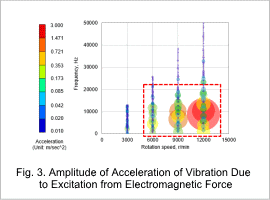
Fig. 2 presents the measurement positions and the radial component of acceleration in cylindrical coordinates at a phase of 0 degrees, displayed as a radar chart. As a measurement example, the graph shows the vibration acceleration at 12,000 r/min corresponding to the fundamental order of the electromagnetic force (2nd electrical order). Additionally, Fig. 3 and Fig. 4 plot the amplitude of vibration acceleration against rotational speed and frequency.
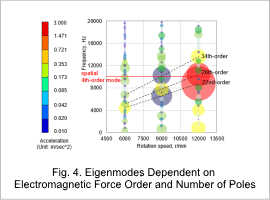
From Fig. 3 and Fig. 4, defining one electrical cycle as the 1st temporal order, it is evident that the vibration acceleration components at the 22nd, 26th, and 34th temporal orders are significant. Furthermore, the vibration intensifies as the rotational speed rises and approaches the natural frequency of the square mode.
Fig. 5 illustrates the vibration modes for the 22nd, 26th, and 34th temporal orders at 12,000 r/min. It can be confirmed that all of these are spatial square modes.
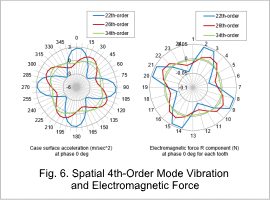
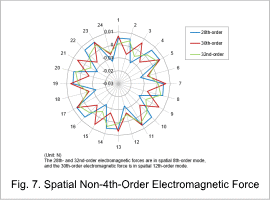
Fig. 6 shows the result of a 2D Fourier transform applied in both temporal and spatial directions to the electromagnetic force acting on the stator teeth at 12,000 r/min. Since the focus here is on the spatial square mode, the spatial 4th-order component lines, including alias components resulting from the 24 slots, are indicated by black dashed lines. Additionally, the temporal 22nd, 26th, and 34th order lines of interest are indicated by blue dashed lines. The electromagnetic force components exhibit high values at the intersections of the black and blue dashed lines, confirming a strong correlation between the vibration acceleration and the distribution of electromagnetic force. This indicates that the spatial square mode vibrations at the 22nd, 26th, and 34th temporal orders are the result of excitation by electromagnetic force. Finally, when the cylindrical radial components at a phase of 0 degrees for the 22nd, 26th, and 34th temporal order components of both vibration acceleration and electromagnetic force are plotted on a radar chart, it is confirmed that they all exhibit the spatial square mode (Fig. 7).