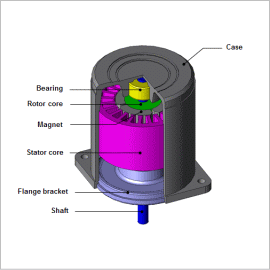
Overview

Electromagnetic force acting on a motor causes vibration and noise in the form of electromagnetic excitation force. Vibration and noise also are produced when this electromagnetic excitation force resonates with an eigenmode of the motor. In order to accurately evaluate this phenomenon, it is necessary to ascertain each frequency and spatial mode in detail about the electromagnetic force and eigenmodes of the motor.
In this example, the acceleration is evaluated by obtaining the electromagnetic force generated in the stator core of the SPM motor at multiple rotation speeds and coupling with the eigenmodes of the motor. In addition, the frequency components of the electromagnetic force and eigenmodes and the spatial modes are analyzed, and the resonance modes are confirmed.

Eigenmodes

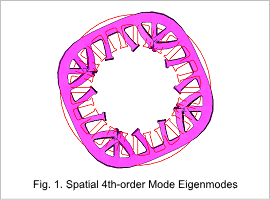
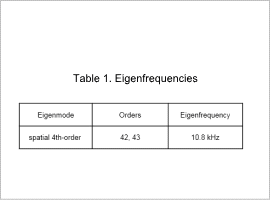
Notice the spatial 4th-order mode is focused on. From the eigenmode analysis results, the eigenfrequency for each vibration mode is found.
The spatial 4th-order  mode results are shown in Fig. 1 and Table 1.

Rotation Speed, Frequency, and Acceleration Graphs

Coupled analysis of magnetic field transient response analysis and structural frequency response analysis is performed to evaluate the acceleration of the vibration excited by the electromagnetic force generated in the stator.
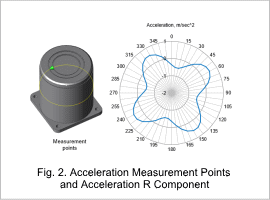
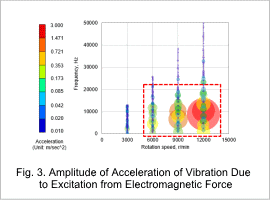
Fig. 2 shows a radar graph of the cylindrical coordinate system R component of the acceleration at a measurement position with a phase of 0 deg. As a measurement example, the graph shows the acceleration computed from the electromagnetic force 2nd-order component. Also, the amplitude of the acceleration is plotted on graphs with axes of rotation speed and frequency shown in Fig. 3 and Fig. 4.
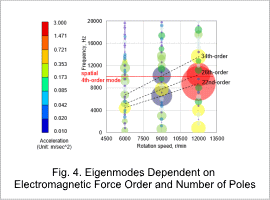
Among the plotted accelerations, some particularly large values can be seen. The electromagnetic forces which are the excitation forces of these vibrations are 22nd-, 26th-, and 34th-order, and the acceleration increases because the rotation speed rises and the electromagnetic force 22nd-, 26th-, and 34th-order frequencies become close to the 4th-order  mode eigenfrequency. This is due to specific frequency components of electromagnetic force strongly resonating with certain eigenmodes.
The 22nd-, 26th-, and 34th-order vibration modes at 12 kHz are shown in Fig. 5. All the spatial 4th-order  vibration modes are shown.
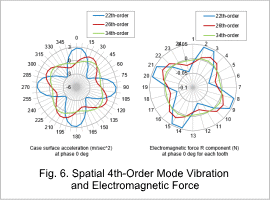
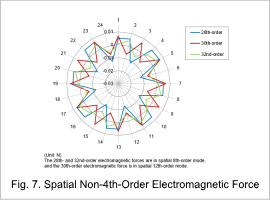
For the 22nd, 26th, and 34th-order components of the electromagnetic force, when the cylindrical coordinate R component at phase 0 deg is shown in a radar graph similar to the acceleration radar graph above, it can be seen that there is a strong correlation between the acceleration and the electromagnetic force (Fig. 6). On the other hand, there are frequency components close to the spatial 4th-order  mode eigenfrequency, but it can be seen that for small order vibrations there are different spatial modes as shown in Fig. 7.