Overview
Motor cores generally use electromagnetic steel sheet. However, engineers are working to take advantage of amorphous and nanocrystalline alloys instead of electromagnetic steel sheet for the core materials in the pursuit of higher efficiency. These alloys are quite expensive though compared to electromagnetic steel sheet, which forces product development teams to choose a material that can satisfy both the performance as well as cost requirements. Optimizations that use materials as design variables are advantageous when selecting the best material while struggling with these kinds of trade-offs.
This case study runs a material optimization of an IPM motor that minimizes the iron losses and material costs to select the best core from three types of materials: electromagnetic steel sheet, amorphous alloy, and nanocrystalline alloy.
In addition, one optimization is also run using only FEA and the other via a surrogate model to compare the Pareto fronts and how much a surrogate model can reduce the time required for the optimization.
Optimization Flowchart When Using a Surrogate Model
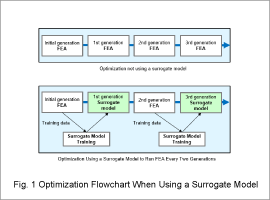
Optimizations using surrogate models replace FEA with a machine learning model for specific generations to obtain results much more quickly.
These optimizations add training data after each generation running FEA to the surrogate model.
Optimization Conditions
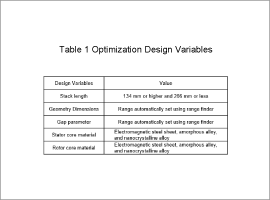
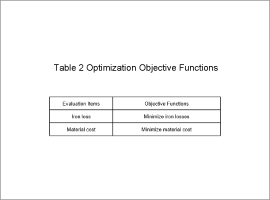
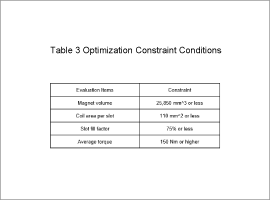
The design variables are outlined in Table 1, the objective functions in Table 2, the constraint conditions in Table 3 and the parametric variables in Fig. 2.
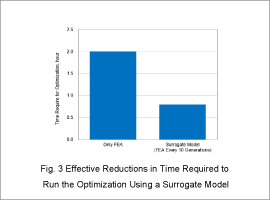
Effective Reductions in Time Required to Run the Optimization Using a Surrogate Model
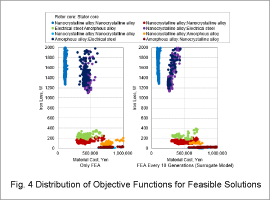
Fig. 3 graphs the time required for the optimization using only FEA and using a surrogate model. Fig. 4 illustrates the distribution of the objective functions for feasible solutions obtained by the optimization.
The graph compares data up to the 130th generation that converges in an optimization that does not use a surrogate model and the data up to the 470th generation that converges for an optimization that does use a surrogate model.
The optimization that does use a surrogate model runs FEA every ten generations.
As shown in Fig. 3, the optimization that only runs FEA every ten generations reduces the time necessary to run the optimization to one-third that of the optimization only running FEA.
As shown by Fig. 4, the optimization only running FEA and the optimization using the surrogate model obtain equivalent results.
Optimization Results
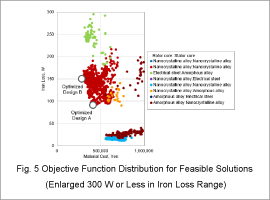
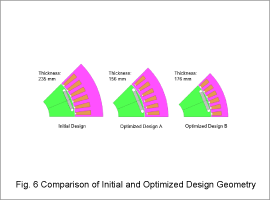
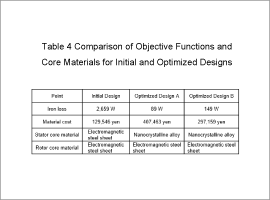
Fig. 5 enlarges the range for the 300 W or less in iron losses from the graph using the surrogate model in Fig. 4. Fig. 6 and Table 4 compare the geometry and objective function values of the initial design and Solution A and Solution B that combine electromagnetic steel sheet for the rotor core and nanocrystalline alloy for the stator core selected from the Pareto front obtained by the optimization.
As illustrated by Fig. 4 and Fig. 5 the distributions of solutions cluster around the objective functions according to the combination of materials. Solutions that use the electromagnetic steel sheet for both the rotor and stator cores have the lowest cost. Solutions that use nanocrystalline alloy for the rotor and stator cores have the lowest iron losses. Solutions that combine different materials for the rotor and stator cores fall in between the lowest cost and lowest iron losses. The solution that uses electromagnetic steel sheet for the rotor core and nanocrystalline alloy for the stator core has lower iron losses and an equivalent material cost as the solution that uses nanocrystalline alloy for the rotor core and electromagnetic steel sheet for the stator core. A design that uses a material with lower iron losses in the stator core is more effective because the iron losses predominately occur in the stator core.
As illustrated by Fig. 6, the design solution with the lower material cost has larger rotor core and smaller stator core geometry, even when compared to solutions with a rotor core that uses electromagnetic steel sheet and a stator core that uses nanocrystalline alloy. That is because the solutions utilize the more expensive material for the stator core.
As outlined by Table 4, The optimization reduces the iron losses to 3.33% to 5.88% of the initial design. These solutions do use nanocrystalline alloy, which is more expensive. However, the increase in material cost rises only about 150% to 280% compared to the initial design.