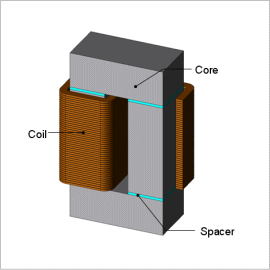
Reactors are used in a variety of electric power systems. For instance, they fill the role of making the current pulsation between an inverter and a motor more smooth. On the other hand, the sound that originates from a resonance phenomenon between an electromagnetic force and an eigenfrequency can become a problem.
The reactor in this analysis has a gap in the magnetic circuit to prevent magnetic saturation. Due to the magnetic fields that occur with high frequency currents, electromagnetic force generates near the gap, and this electromagnetic excitation force in turn causes noise. Vibration and sound grow larger when the electromagnetic excitation force and the transformer’s eigenmode resonate. In order to evaluate this phenomenon with good accuracy, it is necessary to find the electromagnetic force distribution and eigenmode in the high frequencies that become particular problems by using the finite element method (FEM).
This Application Note shows an example of an evaluation of a reactor’s sound pressure when a part of a spacer has been removed.

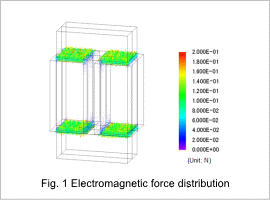
Fig. 1 shows the distribution of the electromagnetic forces. The spacer is made of nonmagnetic material, which means that there are no changes in the magnetic circuit depending on whether or not it has been removed, so the electromagnetic force distribution is the same regardless of whether or not the spacer is present.
From the electromagnetic force distribution shown in fig. 1, it is apparent that the electromagnetic force is concentrated in the gap. This is because the air permeability in the core is different from the gap.

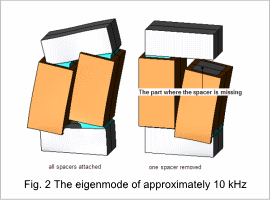
Fig. 2 shows the eigenmode in the vicinity of the fundamental frequency (10 kHz) that carries electromagnetic force. Eigenmode in the vicinity of 10 kHz differs due to the spacers being stripped.

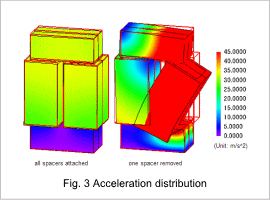
Fig. 3 shows the distribution of the acceleration. The electromagnetic force distribution does not change depending on the presence of the spacer, so differences in the acceleration distribution depend on differences in the eigenmode. Vibrations become larger in the viscinity of the missing spacer due to the spacer being stripped.

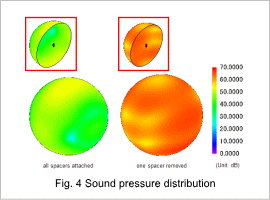
The distribution of the sound pressure is shown in fig. 4. The sound pressure distribution changes depending on the presence of the spacer.
While the core vibrates vertically when the spacer is present, when it is absent, the gap where it is missing vibrates longitudinally, so the distribution becomes dispersed. The vibration is also bigger when the spacer is absent, so the sound pressure gets bigger.