*Please prepare a license ID and password for the license administrator.
*It is different from the service for JMAG WEB MEMBER (free membership). Please be careful.
Overview
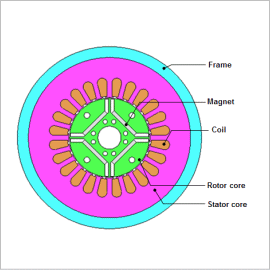
Magnetic steel sheet is used for the cores of drive motors for HEVs and EVs. This is to make them more compact, lighter, and more efficient. The main point for improving efficiency in an IPM motor’s high rotation speed region is how to reduce iron loss. However, shrink fitting is used in order to strengthen the joint between frames and stator cores with laminated structure. The compressive stress generated during shrink fitting is known to increase iron loss. Therefore, it is important to account for the effects of this stress when evaluating iron loss.
Iron loss is generated when there are magnetic-field variations in steel sheet. Also, the amount of iron loss depends on the steel sheet’s iron loss properties. These iron loss properties of steel sheet become worse when it is subjected to stresses such as shrink fitting. The stress caused by shrink fitting has its own distribution, and is particularly large in the back yoke. So, in order to evaluate the iron loss with good accuracy, it is necessary to correctly obtain the stress distribution for the magnetic flux, time variation, and steel sheet.
In recent research, it has been mentioned that in order to increase the precision of stress dependency for iron loss, stress distribution is not the only requirement; evaluations accounting for changes in magnetic flux density over time for each primary axis of principle stress is also a requirement. Based on the results of iron loss with no stress, this document will compare the results of iron loss accounting for only the size of stress, and iron loss accounting for changes in magnetic flux density over time for each principle stress. (hereafter referred to as iron loss accounting for stress tensor)
Iron loss is generated when there are magnetic-field variations in steel sheet. Also, the amount of iron loss depends on the steel sheet’s iron loss properties. These iron loss properties of steel sheet become worse when it is subjected to stresses such as shrink fitting. The stress caused by shrink fitting has its own distribution, and is particularly large in the back yoke. So, in order to evaluate the iron loss with good accuracy, it is necessary to correctly obtain the stress distribution for the magnetic flux, time variation, and steel sheet.
In recent research, it has been mentioned that in order to increase the precision of stress dependency for iron loss, stress distribution is not the only requirement; evaluations accounting for changes in magnetic flux density over time for each primary axis of principle stress is also a requirement. Based on the results of iron loss with no stress, this document will compare the results of iron loss accounting for only the size of stress, and iron loss accounting for changes in magnetic flux density over time for each principle stress. (hereafter referred to as iron loss accounting for stress tensor)
Principal stress distribution
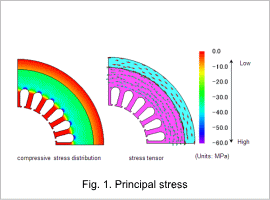
Fig. 1 demonstrates compressive stress distribution and stress tensor for principle stress. It shows that compressive stress occurs in the back yoke and the direction is the circumferential direction. We learn that compressive stress caused by the frame compressing in the radial direction becomes bigger in the slot area. This is because the stress is damped towards the tips of the teeth, while it cannot be damped and concentrates at the slots.
Magnetic flux density (basic wave components) distribution
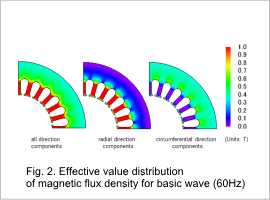
Fig. 2 demonstrates effective value distribution for the basic wave components (60Hz) of magnetic flux density when accounting for stress. The radial direction components of the magnetic flux density are the main components in the teeth, on the other hand, the circumferential direction components are the main components in the back yolk. Upon evaluating iron loss for stress dependencies, these differences in magnetic flux density distribution effect on the methods: if only the stress size is accounted for, or if changes in magnetic flux density over time for each principle stress are accounted for.
Iron Loss Density Distribution
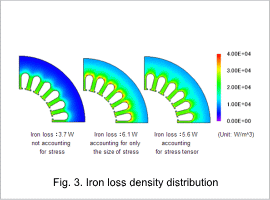
Fig. 3 shows the iron loss density distribution. In order from the left: results of not accounting for stress, accounting for only stress size, and accounting for stress tensor. We learn that depending on if stress is accounted for or not, iron loss density distribution varies, and iron loss values increase approximately 60 percent. This is believed to be due to loss becoming greater from stress, and in order to match iron loss with actual measurements, an analysis accounting for stress due to shrink fitting is required. In the comparison regarding stress dependency methods, differences become visible with an analysis accounting for stress size only and an analysis accounting for stress tensors around the base of the teeth. This is due to magnetic flux density distribution around the base of the teeth greatly affects the radial direction components, and an analysis accounting only for compressive stress can be overestimated compared to an analysis accounting for variations of magnetic flux density over time for each principle stress.


