Here we see a winding diagram for a 3-phase AC induction motor or brushless PM motor (IPM), having 4 poles and 36 slots. This winding could in fact be used with any AC machine, including a synchronous reluctance motor or a wound-field synchronous motor or generator. In most respects it is a regular classical example, and the objective here is to review some of the features of the diagram and its conventions, rather than the winding itself or any particular machine.
The starting-point is the developed winding diagram at bottom left. The term “developed” is borrowed from the geometry of cylinders, and it means that our view of the inside of the stator bore is rolled out on to a plane. We have to imagine that we are inside the stator, somewhere near the centre-line or axis, and looking radially outwards towards the slotted inside surface. If we rotate our view through 360° we will see all 36 slots.
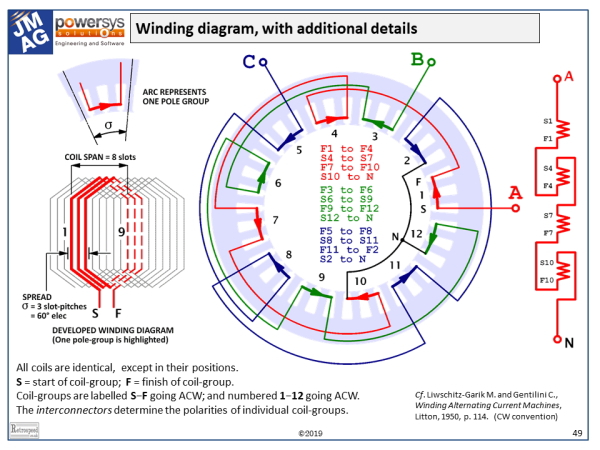
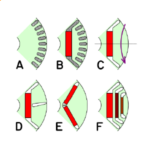
The developed diagram shows only a few slots, but we can see that altogether there are 36 coils. Each coil has two coil-sides, so there must be two coil-sides in each slot. This is what is known as a double-layer winding, one of the most common types. The coils are all identical, and they are laid up so that one coil-side is in the bottom of a slot, and the other at the top near the slot-opening. The bottom coil-sides are shown with dashed lines, because they are hidden behind the top coil-sides when we look outwards from the axis. Each coil is represented in the developed diagram by a polygon with triangular “end-windings”, sometimes called a “diamond coil”.
In machines with many slots the developed diagram can become very intricate, especially when the winding is designed for a variety of series/parallel connections. For this reason an extremely compact form of connection diagram is often used, particularly in winding-shops. In the following, we assume that all the coils are identical, and laid up all in the same direction in a regular fashion; their polarities are then determined by the interconnectors, and what is vitally important in the winding-shop is to connect them up in groups with the correct polarities, in the correct series or parallel paths, and in the correct phases.
The compact diagram shows the pole-groups. In this example with 36 coils, 3 phases, and 4 poles, the coils naturally fall into groups of 3, that is, 36/(3 × 4). One of these groups is highlighted in the developed diagram. Its start point (S) is the leading tail of the first coil in the group, and its finish point (F) is the trailing tail of the last (third). S and F are waiting to be connected to the other pole-groups, according to the main diagram. If parallel connection is intended, the EMFs generated in all the parallel pole-groups must be identical in magnitude and phase.
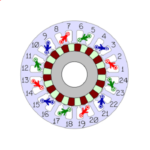
The compact diagram represents each pole-group by a simple arc. So as not to touch or overlap adjacent arcs, the angular extent of this arc (in slot-pitches) is a little shorter than the number of slots per pole per phase, in this case 3 slot-pitches. The number of arcs is equal to the number of pole-groups, and so the number of coils per group equals the number of coils divided by the number of arcs: in this case, 36/12 = 3.
A remarkable property of this diagram is that it is independent of the number of slots and coils. For example, if we substitute a 48-slot stator the diagram does not change, but the number of coils per group increases from 3 to 4. In a 24-slot stator there would be 2 coils per group. All these cases are examples of windings with 60° “spread”, which is extremely common. (Technically we should include the case of 12 slots, but this is degenerate in having a spread of zero). Also note that the diagram gives no information about the coil-span or pitch; thus for example in the 36-slot case a full-pitch winding would have a coil-span of 9, but 8, 7 or 6 could also be used (all with 2 coil-sides per slot).
The arc diagram contains all the necessary information for connecting the pole-groups correctly. With all the arcs in place, it is a fairly straightforward matter of “circuit logic” to connect them up with the correct polarities into the respective phases. To help interpret the connections, a circuit diagram for one phase is added on the right-hand side, and we can see that in this example all the coils in one phase are in series. That is to say, the number of parallel paths is 1. It would be a useful exercise to draw the main diagram again (and the right-hand diagram), with 2 parallel paths and again with 4 parallel paths (the maximum possible number in this example).
The detail is important. The pole-groups are numbered 1 to 12 going anti-clockwise, and every pole-group is labelled S–F going anti-clockwise. Arrows have been added on the arcs, to show the connection polarities, and in the centre of the diagram we have added a written “schedule” of connections: thus for example, “F1 to F4” means that the finish of pole-group 1 is connected to the finish of pole-group 4.
The pole-groups are associated with three phases in this example, and according to the layout the start of phase 2 must be displaced 120° (electrical) from the start of phase 1, in the direction of forward rotation. Since this is a 4-pole machine, that is 60° (mechanical), so if phase 1 starts at slot 1, phase 2 must start at slot 7, and phase 3 at slot 13.
While the arc diagram can deal with windings of great complexity, it does not show the positions of individual coil-sides: these are implicit when the coil-span and the number of coils per group are known, but they are not of primary importance in the process of connecting pole-groups. This might be a disadvantage to an engineer calculating the winding factors or analysing the machine using a finite-element program. Also, the arcs look rather similar to the end-windings sometimes displayed in winding-design software, and this could be seen as a distraction because they have no relation to the end-windings.
For analytical purposes the developed winding diagram is perhaps more useful because it shows the physical position of every coil. When the coils are neatly grouped, as in this example of a distributed winding, the design equations (particularly the winding factors) can be calculated by formulas from the spread and the coil-span; but in other cases, such as concentric windings or windings with fractional slots/pole, matters become more complicated and it may be necessary to assemble the winding factors by Fourier-series analysis on a coil-by-coil basis. Again, there are special cases where completely irregular windings may be used, including coils of different spans, and in such cases the arc diagram is not appropriate.
It is probable that there is no single style of winding diagram that can efficiently represent all the engineering attributes of the wide range of windings used in electric machines. The three elements in the diagram here — the developed diagram, the circular pole-group connection diagram with arcs, and the electrical circuit diagram — are all commonplace but it is not very often that we see them all together, and there are still other representations not discussed here at all. Nowadays the complications tend to arise with both large and small machines having fractional slots/pole, where there is great attention to the EMF waveform, the cogging torque, and the level of harmonic leakage reactance. In preparing a winding diagram with these calculations in mind, the requirements are not quite the same as when preparing an engineering drawing for use in a winding-shop, yet there must be a high degree of consistency throughout all these processes, and ideally a suite of design software should handle all these aspects equally thoroughly.
It is probably fair to say that the main connection diagram (even without the written schedule in the middle) is sufficient for the winding-shop to instal and connect many types of AC winding correctly without using the developed diagram or the electrical circuit diagram. If you are ever lucky enough to be shown round a winding-shop, they may even show you some hand-drawn examples which they use to re-wind machines that are completely burned out. Just hope that you are not the designer of that burned-out machine!
*The diagram comes from the Powersys/JMAG training course in October in Strasbourg