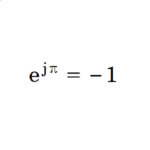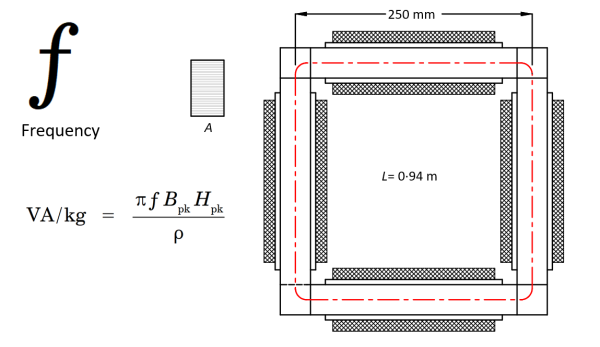
The figure shows a sketch of the Epstein square that is used for the measurement of BH data of laminated core-plate in the form of strips arranged in a square with overlapping ends at the corners. A set of coils establishes a sinusoidal flux-density waveform B in the steel, and the magnetic field strength H is measured. At least under linear conditions, before the saturation becomes extreme, we can consider both B and H to be sinusoidal with peak values Bpk and Hpk. The test is conducted at standard frequencies of 50 Hz and 60 Hz, and sometimes at other frequencies as well.

An important published property of the steel sample is the volt-amperes per kilogramme, VA/kg, and a simple application of Faraday’s law and Ampère’s law in the linear range leads to the formula in the figure, in which ρ is the mass density and ƒ is the frequency.

What is of interest here is the frequency ƒ. If the stack of steel laminations in the Epstein test were the core of a transformer, the equation would tell us that for a given peak flux-density and a given peak magnetic field strength, the volt-ampere capacity of the transformer would be proportional to the frequency.

This significance of this result is enormous. It suggests that if all the power systems in the world raised their operating frequency by 20%, they would require 20% less steel in all their transformers. Given that large power transformers weigh hundreds of tonnes, that’s a lot of steel. The same principle applies to motors and generators, and again the large ones weigh tens or hundreds of tonnes. In the case of AC rotating machines where the speed is related to the frequency, increased frequency could in principle lead to a reduction in size: for the same power, the speed would be greater and the torque less. The torque of an electric machine is essentially related to the rotor volume (and thereby to the stator volume), so in order to save weight it appears desirable to rotate faster, with a lower torque.

Before we jump at the notion of an iron-reducing revolution in the design of power transformers and electric machines, we should take stock of what our predecessors have actually done. We will find that much of the “low-hanging fruit” in the “frequency orchard” has already been eaten. Since the widespread development of AC power, the common frequencies of 50 and 60 Hz have absolutely predominated, even though a few systems were engineered at 40 Hz, 25 Hz, and a few other frequencies. In aircraft power systems for many years we have seen 400 Hz as a standard, which is a direct example of the weight saving predicted by the equation in the figure.  Indeed in many aircraft machines and transformers, special cobalt-iron steels are used with significantly higher peak B and peak H than would be normal in ground-based industrial power systems, and this increases the VA/kg still further.

It can be argued that in a vast number of applications, from hair-dryers to steel rolling mills and wind turbine generators, the common frequency is a compromise that works reasonably well within the engineering and economic constraints that attend an interconnected system. 400 Hz is possible in aircraft only because their power systems are isolated from the grid. And now we are seeing in autonomous, isolated automotive power systems in electric and hybrid vehicles, a predominance of AC propulsion motors operating at frequencies as high as 1,200 Hz. As in aircraft power systems, these are taking advantage of the high frequency to reduce the weight and the size of the motors and generators.

What limits the frequency?

In isolated systems such as EV and HEV automotive powertrains, the operating frequency is limited partly by core losses in the steel laminations, partly by the strength of steel holding the rotor together, and partly by the ability of the power eletronic inverters to supply the necessary high-frequency current with acceptable losses and control characteristics. While we can be sure that the engineers who design these systems invariably optimize their systems as complete packages, it also appears from the wide variety in operating speeds, pole numbers, and maximum frequencies, that there is no single optimum frequency. Even in aircraft power systems, 400 Hz is not universal; there are systems operating at other frequencies including variable frequency and even DC.

On the ground, in large-scale power systems, another important factor is the behaviour of transmission lines and cables. Both of these have inductive series impedance and capacitive shunt impedance, whose effects are proportional to the transmission distance. Over several hundred km, these effects pose serious challenges in the control of the line voltage and the stable operation of generators. A 20% increase in the system frequency would have dramatic consequences in the design and rating not only of the machines and transformers, but also of the ancillary equipment used to control the system voltage, and the protective equipment. Uprooting all of that in favour of a new higher frequency is not as simple as it might seem. Nevertheless, we do see high-voltage DC transmission links being installed in locations where it pays to escape from the constraints associated with 50 or 60 Hz operation; for example, in very long overhead lines or high-power undersea cables. The obvious question is whether isolated wind-turbine generators and other renewable-source generators could run “frequency-wild”, and the answer is that they already do; they simply make use of power electronic conversion to couple to the “mains” frequency of 50 or 60 Hz at a suitable collection point.

As the frequency increases, we have to think about what engineers call the “X/R ratio” — that is, the ratio of reactance to resistance, reactance being the product of frequency and inductance. At 50 or 60 Hz in most power equipment, this ratio is of the order of 10 or more, so that the resistance (which is associated with Joule loss or copper loss) is relatively small, and the cross-section of copper or aluminium conductors can be acceptably small. If we were to raise the frequency we would run into a noticeable increase in skin effect and proximity effect — eddy currents, or the redistribution of current-density within the cross-section of current-carrying conductors. We would also see an increase in parasitic eddy-current effects, such as the losses in transformer tanks, motor frames, shafts, and terminal boxes. These effects are troublesome even now, wherever the cross-sections of conductors or groups of conductors are larger than a certain characteristic dimension. The designers of power equipment have wrestled with these parasitic effects, and many others, for a long time, and it could be said that most of the successful equipment running today is designed in a “frequency sweet-spot”. Of course, design features and sometimes cooling systems have to be adapted so that that frequency really can be classified as a “sweet spot”. In equipment that is directly connected to the mains at 50 or 60 Hz, no matter what the voltage level, the designer has for a long time been forced to optimize the design of the equipment to work with that fixed frequency. The lucky designers working on isolated power systems (such as automotive powertrains) may be free from this constraint, but then the frequency becomes one more parameter to include in a complex optimization project. The fruit of high or wild frequency is not really low-hanging.

What has been particularly exciting in the last couple of decades is the proliferation of “frequency-optimal” systems — not only the completely isolated ones, but also many which are coupled to the mains frequency at some point or other. What was it that made that possible? Power electronics is the answer. What was it that made it effective and efficient? Advances in materials and methods of design and analysis? Absolutely!