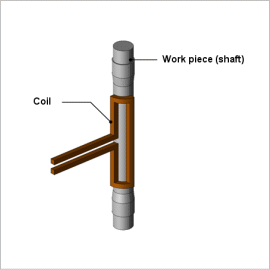
Shafts are used in parts like axles, which transfer power from the engine to rotate the tires, so the need to have sufficient strength to handle the torsion. They also need to have increased surface toughness to raise their degree of abrasion resistance in the areas that join with other parts, and they must maintain their interior toughness in order to obtain strength and fatigue resistance against torsion. By using high-frequency induction heating, which is a type of surface hardening method, the part is heated rapidly on only its surface by a high frequency power source. This process also has many other benefits, such as providing a clean working environment because it uses electrical equipment, being very efficient, and providing uniform results for each product. This is why it is being aggressively implemented in the field.
Eddy currents generated by the high-frequency varying magnetic field occur in the surface of the shaft. The material properties also change due to the rising temperature. Examining detailed phenomena requires handling the phenomena that occur in the interior of the shaft in a numerical analysis based on the finite element method.
This Application Note explains how to create a numerical analysis model and analyze the elevated temperature process in order to use the coil geometry and current conditions (power supply frequency, current value) to verify whether or not the target temperature distribution is obtained.

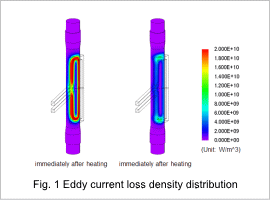
Fig. 1 shows the eddy current loss density distribution produced in the shaft. The magnetic field generated by the coil produces eddy currents in the surface of the shaft. In areas where induction heating makes the temperature exceed the Curie point, the magnetic properties change and both the relative permeability and the electric conductivity grow smaller, which makes the eddy current loss density shrink as well.

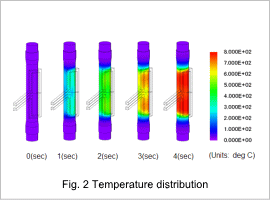
Fig. 2 shows the temperature distribution in the shaft at each time.
From fig. 2, it is apparent that rotating the shaft heats the surface of the shaft facing the coil uniformly in the circumferential direction.