*Please prepare a license ID and password for the license administrator.
*It is different from the service for JMAG WEB MEMBER (free membership). Please be careful.
Overview
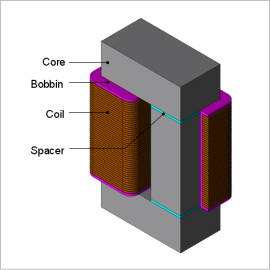
High-frequency reactors used in equipment like DC-DC converters have a high-frequency current accompanying the switching direct current. The reactor’s performance requires a stable inductance in a wide direct current region that is superimposed by alternating current components. If there is only a direct current, the magnetic flux is generated against the external magnetic field, following the magnetic steel sheet’s DC magnetization curve. However, when there is a current waveform whose high-frequency components are superimposed on the direct current component, the response displays a minor loop against the external magnetic field. The values of the inductance in the reactor can have significant differences depending on the method used to measure them. This can make it difficult to carry out a performance prediction during an actual state of operation.
In order to handle the responsiveness of a magnetic field against a current waveform that is superimposed by a higher harmonic with a small amplitude for the direct current component, a magnetic field analysis that accounts for material modeling needs to be carried out. With a magnetic field analysis, it is possible to analyze the machine characteristics from the magnetic flux density distribution.
This Application Note presents the use of the frozen permeability condition to obtain the superimposed direct current characteristic that includes minor hysteresis loops of a high-frequency reactor.
In order to handle the responsiveness of a magnetic field against a current waveform that is superimposed by a higher harmonic with a small amplitude for the direct current component, a magnetic field analysis that accounts for material modeling needs to be carried out. With a magnetic field analysis, it is possible to analyze the machine characteristics from the magnetic flux density distribution.
This Application Note presents the use of the frozen permeability condition to obtain the superimposed direct current characteristic that includes minor hysteresis loops of a high-frequency reactor.
Superimposed direct current characteristics, Magnetic flux density distribution
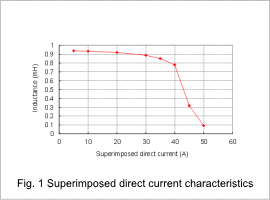
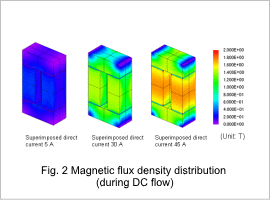
This section shows the superimposed direct current characteristics in fig. 1 and the core’s magnetic flux density distribution in fig. 2 as analysis results of the reactor described.
From fig. 1, it is apparent that the inductance decreases more rapidly as the direct current increases. This is caused by influence from magnetic saturation, as shown in fig. 2.