 Fig. 1
Fig. 1
“In the author’s experience, stray load losses in single phase induction motors are of negligible importance”.
Like many quotations, this is a shocking example of quoting someone out of context. It comes from Cyril G. Veinott, writing in 1935, [1]. That sentence is followed by seven others which completely change the message. Reading only that quoted sentence, the reader could be forgiven for dismissing Veinott as unhelpful at best and ignorant at worst — a disastrous and inaccurate inference, and very unfair. When we read the remaining seven sentences, or indeed the whole paper, we see Veinott’s grasp of the entire subject of loss segregation, in terms of his understanding of the theory, his comprehension of the meaning and validity of test data, and his vision of what further work was needed. Far from making claims beyond his actual work, he makes this humble but emphatic assertion: “Undoubtedly, however, this [point] ought to be investigated and reported upon by others.” We catch a glimpse of Veinott’s mastery.
I dare not copy all the seven sentences here, for fear of copyright infringement, but what I can do is to recommend the reader to buy and read the original paper [1]. Even if you are not interested in the single-phase induction motor, and even if you work on some other class of motor, here you will find a fascinating account that lays the foundation and sets out the rationale and method for loss-segregation testing.
What is loss segregation? And why do we need it?
It’s a question of efficiency. The measurement and calculation of losses helps in the accurate estimation of efficiency. Its importance in this role cannot be overstated. The principles are enshrined in test standards such as IEEE 112 and IEC 60034 and many others. The test standards are themselves important because they address the vital subject of energy efficiency on a global scale, and they are under constant review to improve methods and reduce uncertainties.
It is also a question of product design. It is obvious to motor designers that if there are power losses in a machine, we need to know their individual origins. We need to know how to calculate them, how to measure them, and how to reduce them. “Loss segregation” is the process by which the separate loss components are identified, usually through defined test procedures and generally supported by calculation.
There are of course many different loss components in a machine : stator and rotor Joule loss, core loss, friction and windage, and others. “Others” doesn’t sound precise, so we use the term “stray load loss”. Actually all these labels require more precise definition than just a name, to provide a proper basis for measurement and calculation.
Precise definition isn’t easy. Let’s take the stator Joule loss, which can be expressed as the number of phases times RI2, where R is the phase resistance and I is the RMS current. This looks simple enough, but what if the phases are not perfectly balanced? How accurately can we measure the resistance R? How accurately can we calculate it? Given that resistance is a function of temperature, and that winding temperature is not uniform throughout the whole winding, and that the conductivity of magnet wire after winding is not necessarily known with great precision, it’s easy to see that complications affect even the simplest of the loss components. In the case of the rotor Joule loss, in a polyphase induction motor it can be inferred from the slip and the sum of the output power and the friction and windage, without knowing the rotor current or the rotor resistance; but this applies only under balanced conditions and it is indistinguishable from the rotor core loss at asynchronous speeds.
In Veinott’s case this simple method of inferring the rotor Joule loss could not be used, because it does not apply to the single-phase induction motor. He therefore had no option but to estimate it by calculation, even at no-load. This required a full understanding of the cross-field theory which had been expounded in 1924 by H.R. West and the revolving-field theory described by Kimball and Alger, also in 1924. These theories are by no means easy, and their implementation in complex numbers with a slide-rule was particularly awkward (and still is). Writing in 1935, Veinott would have been about 27 years old, and his mastery of these methods is characteristic of his stature as an engineer.
Veinott defined the core loss as the no-load core loss, so that any additional core loss under load would fall into the category of stray-load loss.
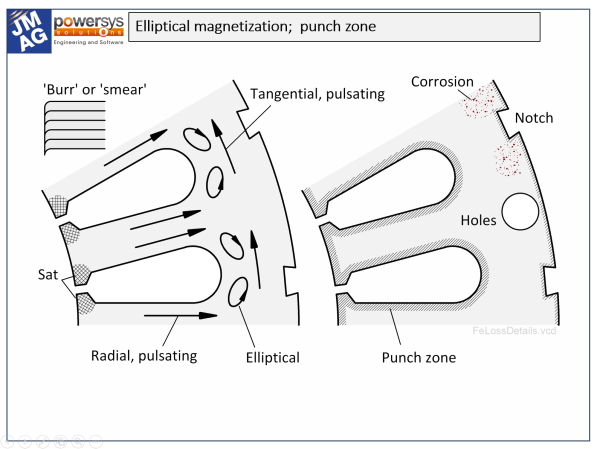
Let’s look into it. Figure 1 shows part of a lamination. We can get formulas and graphs and tables of “core loss” from steel manufacturers. They measure this data very carefully in the laboratory on defined samples of steel: usually, stacks of strips or rings magnetized under AC conditions with sinusoidal flux-density waveforms, and instrumented to measure loss density as well as the BH curve. The composition and heat-treatment of the steel is carefully controlled and specified. All this is prescribed in the IEEE and IEC and JEC standards and many others.
We motor people buy this steel rolled up in heavy bales. We unroll it. We flatten it, pickle it, slit it, stamp it, coat it, anneal it, assemble it into core-packs, weld it, clamp it, and shrink-fit it into a housing. For cage-type induction motors we pour molten aluminium (or worse, copper) into the core-pack under pressure, often without stopping to ask whether any impurities from the steel migrate into the aluminium, or vice versa.
Finally we machine the outside to make it clean and round and shiny. Sometimes we subject it to induction heating and then immerse it in water to break any unwanted contact between the laminations and the aluminium. With the assembled machine we often operate with flux-density waveforms that are not sinusoidal and not even at the same frequency as they were in the laboratory core-loss tests.
What happens? We get stray-load loss. It’s not surprising. Figure 1 shows some (but not all) of the departures from ideal core-loss conditions arising purely from the design and manufacturing. The laminations have holes, flats, and notches as well as slots; around all these there is a “punch zone” where the magnetic properties are degraded. We have regions of intense saturation in tooth-tips and slot-bridges. We may have “burr” or “smear” at the stamped edges. We may have corrosion. And we generally have regions where the flux-density vector is rotating or precessing elliptically, giving rise to “rotational” loss. We also have residual and sustained stress distributions, and in high-speed machines also dynamic and variable stress distributions, which affect the losses.
We can see that the carefully-prepared core-loss data cannot be expected to be reliable under the conditions we have just described. Where can we find look-up tables for stray-load loss? We cannot find them! (It is true that some of the standards assign a value to the stray-load loss, in terms of a percentage of the total power; but this is derived from statistical surveys, and is not helpful in the design process per se).
Over the years there have been many attempts to calculate the stray-load losses using classical theory. Two notable examples are Alger et al [1959] and Christofides [1965], although there were many studies of “surface losses” long before these. Remarkable and useful as these studies were, they involved many approximations and in particular they were working with estimated flux-density waveforms which today we would see as quite crude. Harmonic analysis was used to a very limited extent; but saturation was almost completely ignored, and this would be seen as inadequate nowadays, especially in highly-rated machines.
When we set this history against modern practices with extreme ratings in an environment of great pressure on efficiency, it is easy to see why the most sophisticated calculation methods are essential. To illustrate this, Figure 2 shows a finite-element calculation of core-loss. My purpose here is not to explain how to do this calculation, but to underline the reasons why we need it.
While core loss (and many components of stray-load loss) can be calculated using modern numerical methods, the engineering analysis does not stop there. Obviously the ventilation and cooling losses must be calculated as well as the temperature distribution, and this leads into a domain of mechanical engineering at least as complex as the one we have been considering. A simple example of this is the fan loss arising in motors with shaft-mounted fans; traditionally it would be included in the friction and windage. That does not seem too challenging at the level of testing, but how to calculate the fan loss? That’s another story.
So far this discussion has been biassed towards analytical engineering, but some of the loss components are beyond the scope of accurate calculation. Therefore, complete control of the loss-generating mechanisms must include physical experimentation and deep knowledge and skill in factory process engineering. This is an area where there needs to be a close relationship between high-level analysis and high-level process engineering.
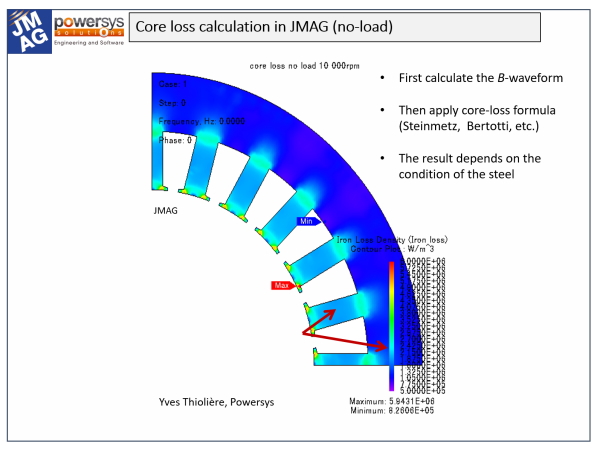 Fig. 2
Fig. 2
One of the obvious aspects of this is the properties of the materials. How do we know the properties of electrical steel at every point in a machine? How do we know the contact resistance at every point between the conductors in a cage-type induction motor and the surrounding laminations? The answer is that we don’t know this data with absolute precision. What we have instead is a set of parameters with engineering tolerances defining or limiting the degree of variation (or the degree of uncertainty). This is a worthwhile subject for more research. So much of what we publish on advanced topologies or methods of calculation rests on simple assumptions about the properties of the materials, without any justification or consideration of the effect of variations. So much development effort is made with new materials, while it is quite possible that we neglect the full understanding of old materials and the processes in which we use them.
As an introduction to the important subject of loss segregation, like many others before me I would recommend Veinott’s 1935 paper. He doesn’t describe the test methods. In most respects they are the same as those which we use today, except for the expected improvement in instrumentation. The key concept in Veinott [1935] is the strategy: the combination of measurement and calculation, and the insight into factors which at the time were poorly understood. All of this is just as relevant today as it was then, and most of it applies to every class of electric machine. Of course not only the instrumentation but also the methods of calculation have developed immeasurably beyond what was available when Veinott described the basic principles.
- [1] Veinott C.G., Segregation of Losses in Single Phase Induction Motors, Electrical Engineering, pp. 1302-1306, 1935.
- [2] West H.R., The Cross-Field Theory of Alternating-Current Machines, Trans. A.I.E.E., pp. 466-474, 1926.
- [3] Kimball A.L. Jr. and Alger P.L., Single-Phase Motor-Torque Pulsations, ibid., Vol. 43, pp. 730-739, 1924.
- [4] Alger P.L., Angst G. and Davies E.J., Stray-Load Losses in Polyphase Induction Machines, ibid., Vol. 78, No. 3, pp. 349-355, 1959.
- [5] Christofides N., Origins of load losses in induction motors with cast aluminium rotors, Proc. I.E.E., Vol. 112, No. 12, pp.
2317-2332, 1965.