Fig. 1 Two coils

One of my teachers (Dr. Thomas Foord) gave undergraduate lectures that were so clear, I feel as though I could repeat them nearly 55 years later. Of course I could not do it. That teaching gift is given to very few. Yet it seems to remind us of the enormous importance of the teacher, in an age when so much of the limelight goes to inventors and researchers. The teaching function goes hand-in-hand with scholarship, and if we look back to the academics and many of the industrial engineers of the past, the art of study and the art of teaching were prominent in their contributions. It has even been said of Euclid that his primary genius was as a teacher [3].

Shortly before Dr. Foord died he gave me his most treasured books, and one of them was a tattered copy of the U.S. Bulletin of the Bureau of Standards, published by the Department of Commerce and Labor in Washington D.C. in 1912, ‘Formulas and Tables for the Calculation of Mutual and Self-Inductance’. Its 237 pages are packed with formulas for the calculation of inductance, and the depth of scholarship is clear on every page, with names such as Maxwell, Rayleigh, Weinstein, Nagaoka, Kelvin, Neumann, and many others generously cited.

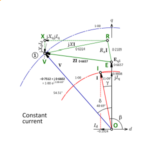
Fig. 1 does not appear in Rosa and Grover [1912]. (See [1]). But it is drawn in the style of some of their diagrams. It represents two concentric coils which may be circular or rectangular, and we can see the orderly arrangement of the turns with insulated wire. Of course the insulation introduces space between the conductors.

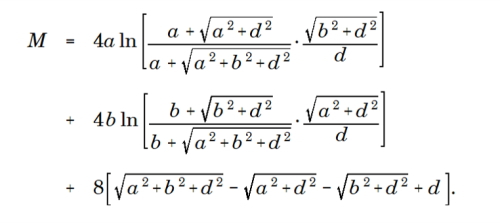Fig. 2 An inductance formula from Rosa and Grover

Coils of this general type are common in electrical engineering and they almost always have a multiplicity of turns. To calculate the self- and mutual inductances, one approach would be to calculate the self-inductance of each turn, and the mutual inductance between every pair of turns, and put the results into a square matrix. This matrix can then be reduced to a 2 × 2 matrix by multiplying it by a suitable connection matrix and then post-multiplying the result by the transpose of the connection matrix. This technique involves a lot of tricky computation but it can be formulated and programmed. Indeed in power-systems analysis it is a common method. It seems to have been developed by Gabriel Kron in the 1940s [5], and the timing of that is interesting because Kron is often said to have been a visionary who foresaw the computer age, yet the works of Rosa and Grover were nearly half a century earlier.

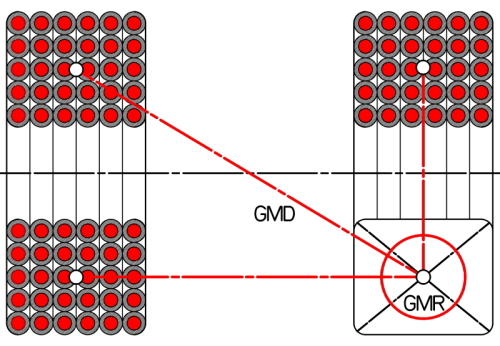
The engineers of Rosa and Grover’s era, and their predecessors going back at least as far as Maxwell and Rayleigh, certainly did not have computers and yet they were not afraid to tackle problems of such complexity. One of the key ideas they used for multiple-conductor configurations was the idea of the geometric mean distance (GMD) of one group of conductors from another group. A related concept is the GMR or geometric mean distance of a group of conductors from itself. These ideas are shown schematically in Fig. 1. The GMD and GMR can be calculated by relatively straightforward processes, and they are even tabulated for some common cases. What they do, in effect, is to ‘coalesce’ groups of conductors into single units with a defined cross-section area.

With them, it becomes possible to write formulas for self- and mutual inductance which are relatively easy to program and calculate. Fig. 2 shows an example from Rosa and Grover. I’m not going to associate it with Fig. 1, because I don’t want to make a mistake and I don’t want to steal the thunder from Rosa and Grover. My message is simply to bring this extraordinary simplification into focus, and recommend the reader to study the original works.

Complications were considered. For example, the spacing between conductors requires the introduction of second-order corrections, some of which are attributed to Maxwell. The coils may not be concentric; their axes may not be aligned; and the turns may even be helical. They may have different dimensions. But the principles hold for all such cases, even though some of the formulas become very complicated. The formulas often involve infinite series, and it was necessary to consider the convergence, and the range of dimensions for which the formulas were valid.

Going back to the earliest times, accuracy was considered highly important. When Grover wrote a more digestible summary of the subject in 1946 [2], he said that ‘one part in 1000’ was generally the aim, although in many cases it was much better. How could they test the accuracy, 120 years ago?

One approach was to compare formulas by different scholars, and Rosa and Grover do this with great diligence, even to the point where they recommend the use of one formula or another in different circumstances. Another approach was to design and construct calculable or nearly-calculable inductors, which could be measured with the finest instruments of the time. Fluxmeters and galvanometers arranged in special bridge circuits were developed from early times, and the accuracy of some of the historic measurements would surprise many modern engineers; [4].

It’s interesting to consider how such inductance calculations would be performed using a finite-element system. In one sense the finite-element method takes the GMD/GMR approach to another level, by integrating vector potential over coil-side regions, especially in the confines of slots in electric machines where the effects of insulator spacing may often be somewhat ‘washed out’. But in air-cored coils and overhead transmission lines, or in cable trays or even on printed circuit boards, what exactly is the best approach?

I must admit I don’t know the general answer, or even if there is a general answer. I set out to write the diary with some thoughts of admiration for the great minds of the past, but we can be sure there are minds of equal analytical capacity in the business today, and I’m sure they have many of the answers.