The idea in the finite-element method is to divide a difficult problem into a number of simpler problems which can be solved simultaneously; the solution to the difficult problem is then obtained by combining the solutions to the simpler problems.

This description encompasses the three canonical stages in the finite-element process as we know it today : pre-processing (the division into a number of simpler problems), then solving, and finally post-processing to obtain the overall result. In sophisticated software tools such as JMAG the post-processing includes further manipulation of the basic solution to provide graphic images of the solution and engineering parameters. Often these are defined by the user, as we know.

The idea of division and re-assembly is very old, and many instances of it can be found in mathematical analysis; it could even be said to be the basis of the differential calculus. Several graphic examples can be found in the mensuration of the circle, as in the left-hand figure. We can find this diagram in the Kaisan-ki Kōmoku of Mochinaga and Ōhashi (1687), described by Smith and Mikami [1914] as a “crude method of integration that characterized the labors of the early Seki school”.

As an engineer I’m not so sure I would use the term “crude”. I would rather describe it as “remarkably effective”. Obviously the more elements, the greater the accuracy. Of course what seems obvious to an engineer may not be completely straightforward mathematically or computationally, and this was equally true in the 17^th century. Methods such as the one suggested in the left-hand figure were used to estimate the value of \( \pi \) to an extraordinary number of decimal places, and one of the most distinguished contributors was Takebe Kenko (1664-1739), who also developed methods for mensuration of the circle using infinite series. An infinite series is a sum of elements, so to speak, and in this sense it could be described as a “finite-element” method.

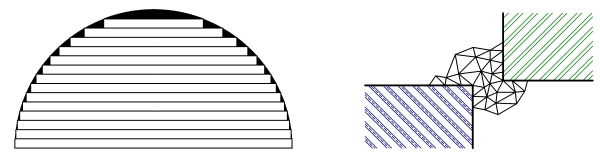Fig. 1 Finite elements

The right-hand diagram is intended to show the division of a “field problem” into a finite number of small triangular elements. A field problem is a region of space in which we need to know the distribution of such quantities as flux-density or temperature. From the 18^th to the 20^th century such problems were analysed by methods based on the differential calculus, often with extraordinary mathematical ingenuity and sophistication. Most problems were restricted to single regions of the same physical material, and any nonlinearity in material properties made matters much more difficult. The computation of the practical solution often involved infinite series, and it can be said that the mathematical manipulations could, in places, obscure the physical process to some degree. The computation was also very labour-intensive.

Along comes the digital computer in the middle-to-late 20^th century. The labour of calculation now takes on a different character. Of course if we have enough computer capacity the cost of laborious calculation becomes low. But digital computers are basically restricted to binary arithmetic, and so there has to be a transformation of the piecewise-continuous, nonlinear field problem into binary arithmetic. That immense task is what the software does.

The right-hand figure also shows another feature that we often take for granted. The “subdivision into simpler problems” evidently starts with a mesh of triangular elements, and it appears that this mesh has no difficulty in conforming to the awkward shape presented by the two corners of the blocks of material on either side. Such corners are common in engineering, yet they cause problems for classical analysis because of singularities at the extreme points. Of course the mesh may be refined near these points, but the engineer using a finite-element tool never has to stub his or her toe on such a singularity.

The ability of a triangular mesh to conform to material boundaries and interfaces of arbitrary (and often awkward) shape is one of the reasons for the predominance of the finite-element method, especially over earlier competitors such as the finite-difference method which was much less flexible. It’s remarkably effective!

Reference : Smith, D.E. and Mikami, Y., A History of Japanese Mathematics, The Open Court Publishing Company, Chicago, 1914 (reprinted in Forgotten Books Classic Reprint Series, ISBN 978-1-330-04256-4, 2017).