Fig. 1 Animations — snapshots from (A) Video 44 and (B) Videos 46 ‐ 48

The educational and commercial importance of animation can hardly be overstated. We see it almost everywhere, and it now has a significant role in even the most traditional areas of education.

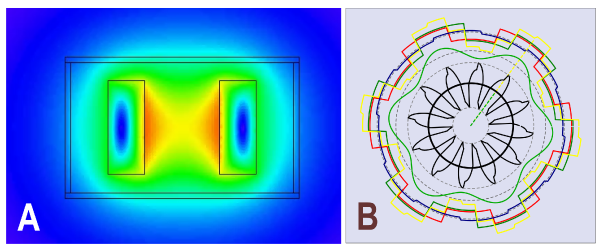
The example in Fig. 1A seems (in Video 44) to be the most natural way to visualise the dynamic relationship between the current in a pair of bus-bars and the entire magnetic field around them. In the preparation of this video, it arose almost by accident as an easy implementation of JMAG’s native facility to export animations of field solutions.

The example in Fig. 1B (Videos 46 ‐ 48) is quite different. It required the preparation of a separate computer program for the specific purpose of illustrating some of the properties of Fourier series in relation to the torque production in AC machines.

In this Engineer’s Diary I would like to reflect on the process and purpose of producing these animations. I see the videos as a teaching exercise. They are also an exercise in self-learning, because in writing them I have to clarify my ideas and develop them into a story. I must also check (as far as I can) that they are rigorous. They are not part of a formal curriculum, but they belong to a loose association of topics in the theory and design of electric machines. I’m sure many engineers share these methods.

The animation part was so easy.

But the technical content is far from trivial. In Video 44 we see (quite literally) a series of solutions of Maxwell’s equations in a transient 2-dimensional nonlinear boundary-value problem; but the solution itself and the means of displaying it are both the result of half a century of development in numerical analysis and computing (including the hardware as well as the software). The scale and extent of these developments are so vast as to be hard to imagine. A generation ago, we didn’t have them. The nearest thing to animation was a pencil-sketch on a scrap of paper. So perhaps the most astonishing aspect is the fact that the animation part was so easy.

In Videos 46 ‐ 48 I needed to apply my own knowledge of Fourier series as it applies to the production of torque and the waves of ampere-conductors around the air-gap of an AC machine. It took a long time to grasp these ideas. My first introduction to Fourier analysis was as an apprentice in a grimy factory in about 1968, learning about the high-frequency induction-welding of steel tubes. At that time I also learned the rudiments of Fortran programming (using punched tape for input and fanfold paper for output). Desktop monitors were more than a decade in the future, so the pencil-sketch was an essential part of one’s kit. So again, perhaps the most astonishing aspect is the fact that the animation part was so easy.

But if the animation part was “so easy”, what about professional technique and best practice in the design and production of videos with animation? I have to hold up my hand: I have no training or expertise in these matters. Realising that I might have “raised my head above the parapet”, I made a quick internet search for “the use of animation in engineering education”, and was immediately overwhelmed by the scope and extent of serious discussion and analysis of this important topic.

One particularly helpful introduction was an article in The Times Higher Education by Dr. Nigel Bairstow [1], from which I have quoted (with permission) this extract:

Thankyou, Dr. Bairstow and The Times Higher Education!

But then the curmudgeonly stick-in-the-mud throwback-monger spoke up in my aging mind.

These graphic displays are entertaining and they certainly show some interesting points. But they are nowhere near as powerful as the mathematics or the engineering theory behind them. By themselves, they do not produce any calculated values: they do nothing more than to illustrate them. In fact we have had to use the mathematics not only to create the displays but also to interpret them. Not only the writer but also the reader needs the engineering theory to understand them and to put them to practical use.

In teaching undergraduate engineers I would be wary of using animated displays like these, for fear of presenting the subject like a cartoon show, and dumbing it down by hiding the mathematics. I imagine that bright students are not going to be impressed by gimmicky animations produced by an amateur (no matter how authoritative or distinguished the academic credentials behind them). Students need and want the beef, not just the sizzle. They pay so much in cash and in precious years of their lives: they deserve to acquire skills, not merely to be entertained. But if animations help to clarify one or two tricky concepts, they deserve a place in the curriculum.

For seasoned engineers, it’s a different ball-game. Already trained, already skilled, already experienced, they may use animation as a regular daily tool to see further into their calculations, and to share and explain them to colleagues and customers. That’s where a facility such as JMAG’s Export Animation will come into its own, while the Fortran animation of Fourier series (Fig. 1B) may be useful only in seminars or classrooms on electric machine design. Or possibly in a JMAG video (I hope!)

It may be that the whole operation of AC machines can be expressed in terms of words and dynamic images — in other words, in animations — but when we come to design or analyse a machine in real life we really have to use the mathematics, or at the very least, some competent form of software that programs the appropriate mathematical methods. It’s true that on the factory floor you will meet engineers who have the whole design and operation in their heads: no mathematics, no computer graphics — but animation in their mind’s eye.

To summarise, we are lucky nowadays in having three modes of expression for our electrical theory:

The early pioneers in electrical engineering (indeed in all fields of engineering) had only the first of these — maybe even none of them.

The computer graphics enrich our understanding especially if we use them to exercise our imagination as to what is going on in the machine; but they are nothing more than a little helper. So far from using these displays in teaching an undergraduate class, I might suggest a student project to write such a display. I’m sure there are many bright students who could do a better job.

Further reading

[1] https://www.timeshighereducation.com/campus/animating-education-teaching-tool-brings-learning-life
Dr. Nigel Bairstow, University of Sydney, in The Times Higher Education, 22-Nov-23.