FEAが設計現場にもたらす効果とは何か?
電磁界有限要素解析(Finite Element Analysis:FEA)はここ15年ほどの間、開発現場において採り入れられるようになり、急速な広がりを見せました。
その用途は現場のお客様の開発ニーズに応じて様々ですが、なぜFEAはそれほどの広がりを見てきたのでしょうか。また開発現場におけるFEAの効果とはいったいどのようなものなのでしょうか。
この小稿では、本年度一年間の予定でFEAの持つ特徴を多角的な視点から捉えることで、FEAが開発現場にもたらす効果についてご紹介して参ります。
1.はじめに
前号では、近年目覚しい進展を見せるFEA(Finite Element Analysis)について、その普及の背景をご紹介致しました。FEAが設計現場に広く浸透した理由の一つとして、解析計算による物理現象の高い再現性が挙げられます。
今号では、このFEAの特徴とも言える高い再現性を実現できている理由を考えてみたいと思います。
2.なぜ高い再現性を持つのか -分解能の視点から-
FEAは解析対象を分割された要素の集まりであるメッシュとしてモデルを表現します。また、時間的に変化する入力波形や非線形性を持つ材料特性は点列などのデータとして表すことで定義できます。FEAはメッシュや入力波形の詳細度を上げることで分解能の高い解析が可能であり、このことが物理現象に対する高い再現性を有している理由だと考えられます。
本節ではこの高い分解能を可能にしている理由について、以下の4つの視点から明らかにしてみたいと思います。
- モデル形状の視点から
- 支配方程式の視点から
- 材料特性の視点から
- 駆動条件の視点から
2-a.モデル形状の視点から
電機機器の形状は設計上の制約条件を考慮しながら、望ましい出力特性が得られるように工夫が凝らされています。たとえばモータでは、ロータとステータ間におけるギャップ構造が出力特性に大きな影響を及ぼしますし、設計上のノウハウが凝縮されている箇所の一つです。リラクタンスモータのように磁気的突極性を利用したモータでは主磁路上のわずかな形状の違いが特性に大きな影響を及ぼします。また図1に見られるように、ティース先端にくぼみを入れた形状をもつモータのコギングトルクはくぼみのない形状に比べて大きく低減していることがわかります。
簡易設計によく用いられる磁気回路法では、磁気回路を構成する部品ごとに磁気抵抗を積分計算しますが、形状が複雑になると、精度を上げるためには必要とされる部品の計算数が非常に多くなります。
このため、予め計算に必要な部品を選択することが必要となり、熟練設計者の勘と経験に頼らざるを得ません。また複雑な形状の場合、初等的な積分計算では磁気抵抗の算出が困難な形状も存在しますので、扱える形状には制限があります。
これに対してFEAはCAD図面などの形状データに即してモデル化することが可能です。
FEAは対象を有限の要素に分割して要素の集まりであるメッシュとして形状を定義します。(図2参照)解析対象のメッシュモデルは、形状データさえあれば、メッシュの自動生成機能などを用いて生成することができますので、解析対象の形状や利用者のスキルを選びません。
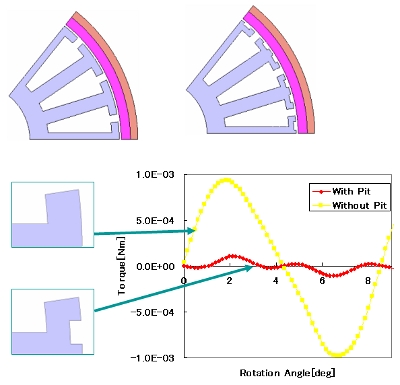 図1 くぼみあり/なしのティース形状とコギングトルクの比較
図1 くぼみあり/なしのティース形状とコギングトルクの比較
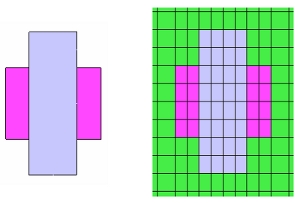 図2 電磁石モデルの形状と離散化後のメッシュ
図2 電磁石モデルの形状と離散化後のメッシュ
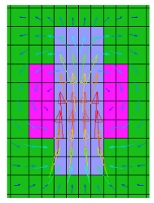 図3 電磁石モデル(図2)における要素ごとの磁束密度分布
図3 電磁石モデル(図2)における要素ごとの磁束密度分布
2-b.支配方程式の視点から
マクスウェル方程式は電磁現象を支配する基礎方程式であり、実測の結果に対する再現性の高い解析を実現するには、この方程式を近似することなく正確に扱う必要があります。マクスウェル方程式は時間微分、空間微分を含む偏微分方程式で表され、対称性がよくかつ簡易な形状でなければ、手計算のみによる正確な解析は一般に困難です。さらに非線形磁化特性や導体を考慮した解析では数値計算による解析が必須となります。
FEAは多数の要素から構成されるメッシュにより形状が定義された解析モデルに対して、マクスウェル方程式を要素単位で適用して解析します。この結果、FEAでは磁性体における磁束密度分布や導体中の電流分布だけでなく、磁性体周囲の漏れ磁束や近接効果を含む渦電流分布などすべて考慮した状態で解析されます。FEAでは実機の測定状態に即した状態で解析結果が得られますが、これは解析対象をそのままモデル化して方程式を直接適用するというFEAの持つ原理的な特徴といえます。
磁気回路法で、漏れ磁束を考慮した解析を行うことは不可能ではありませんが、予め漏れ磁束の影響を考慮した磁気回路を構成して解析する必要があります。このため解析精度は設計者のスキルにより大きく左右されますが、FEAでは、空間部分も含めて生成されたメッシュの各要素に対してマクスウェル方程式を等しく適用されますので、利用者のスキルに拠らない結果を提供することが可能です。
2-c.材料特性の視点から
モータやトランスをはじめとする機器は磁性体から構成されるため、磁化特性が出力特性を大きく左右します。磁化特性は磁気飽和により著しい非線形特性を有しますので、これを正確に考慮して精度よく解くことが、測定結果との間の高い再現性を得るための必須条件となります。
FEAでは、ニュートン・ラプソン法に代表される非線形計算手法を用いることで、実際の磁化特性を考慮した解析が可能です。(図4参照)要素ごとに動作点が求まるため、磁気飽和による複雑な磁束密度分布や励磁電流を変えた場合の磁束密度分布変化も正確に捉えることができます。磁気回路法でも、磁気飽和を考慮した解析は、起磁力ごとに各磁性体の磁気抵抗のテーブル値を用意するなどにより可能ですが、FEAのように任意の磁化特性に対応して解析するような柔軟性はありません。また導体中に渦電流が発生する現象を扱う場合には、導体部分に電気伝導率を指定することで、渦電流を考慮した解析が可能ですが、磁気回路法ではそもそも分布量を計算しないため、渦電流の効果を取り込むことは困難です。
次号でご紹介する予定ですが、たとえばリレースイッチなどでは、コアに生じる渦電流が応答特性に大きな影響をもたらすことがあります。コアの磁化特性に加えて、コアの渦電流も同時に考慮する解析では、FEAのような解析でなければ、定性的な評価も困難となります。図5と図6に電磁リレーの鉄心における渦電流分布と変位の応答特性を示します。
また実際の現象では渦電流損失などによる昇温効果のため、機器がその動作点において明示的な温度依存性を示すことがあります。このような場合には電気伝導率などの材料特性に温度依存性を考慮した解析が必要になります。これについては電磁界解析のFEAと熱解析のFEAを組み合わせることで、温度依存性を考慮したFEA解析も可能になりますので、測定結果との比較において高い再現性が期待できます。(IH調理器のような上記現象を積極的に利用した機器もあります)
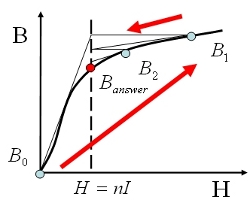 図4 ニュートン・ラプソン法の収束イメージ図
図4 ニュートン・ラプソン法の収束イメージ図
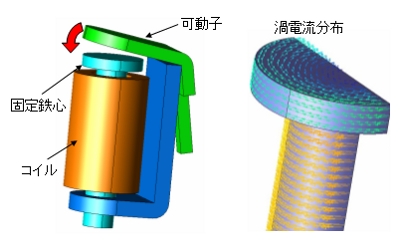 図5 リレースイッチにおける渦電流分布
図5 リレースイッチにおける渦電流分布
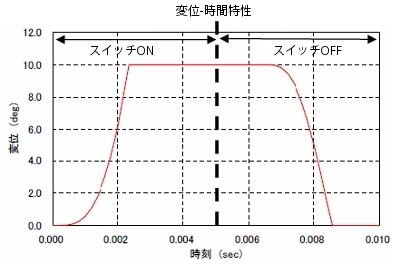 図6 リレースイッチにおける変位の応答特性
図6 リレースイッチにおける変位の応答特性
2-d.駆動条件の視点から
電磁現象を扱う際に起磁力源となるのが磁石や電流です。物理現象に対する再現性の高いシミュレーションを実現するには、駆動条件を実機の状態に合わせて設定できる、高い分解能を持った条件設定が要求されます。
起磁力源として磁石を用いる場合は、FEAでは磁石の磁化特性だけでなく、複雑な着磁パターンも要素ごとに磁化分布を定義できますので、実際の磁化分布に近い詳細な状態を反映させることができます。磁石の着磁状態はコギングトルク波形や誘起電圧波形に大きな影響を及ぼしますので、これらの評価にはFEAのような分解能の高い設定が可能であるシミュレーションが不可欠となります。図7にSPMモータの磁石着磁パターンのみを変更したときのコギングトルクと誘起電圧を比較した結果を示します。この結果から、同じ磁化特性であっても着磁パターンの違いが波形に定性的な違いをもたらしていることが分かります。
起磁力源として電流を用いる場合は、通電される電流波形が既知の場合とそうでない場合で扱いが異なります。電流の正確な時間変化がわかっている場合は、電流値を時刻テーブル値として入れて解析をすることができます。
しかし多くの場合、解析対象には電源を含む駆動回路が取り付けられており、電流は解析対象と駆動回路を含めて決定されることになります。このような場合は、予め入力すべき電流波形がわからないため、回路を含めたFEAによる解析が必要となります。回路は回路方程式により厳密に定義されますが、これをマクスウェル方程式によるFEAと連成して解くことで、駆動状態を詳細に考慮した解析が可能になります。
図8に駆動回路を含む電磁弁モデルを回路連成により解いた時のキャパシタンスの充放電前後の電流の時間変化を示します。充電ののち、スイッチの切り替えによりLC振動を伴う電流が発生していることがグラフから読み取れます。
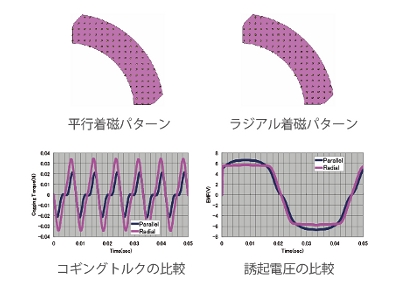 図7 コギングトルクと誘起電圧の比較結果
図7 コギングトルクと誘起電圧の比較結果
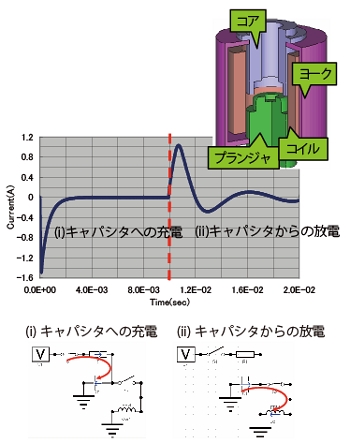 図8 回路を含む電流の応答波形(電磁弁)
図8 回路を含む電流の応答波形(電磁弁)
3.まとめ
以上のようにFEAはその手法上の特徴から原理的に測定結果を高い精度で再現できる解析手法であることがお分かり頂けたと思います。
FEAでは、基礎となるマクスウェル方程式を基本とした電磁現象だけでなく、運動を考慮することで生じる速度起電力の効果なども容易に取り込むことができます。これらと外部回路を組み合わせた解析により、実際の運転状態に即した状況を再現したシミュレーションを実現することができます。
次号ではこの特徴をフルに生かして解析された事例を通して、FEAの効果を具体的に見て行きたいと思います。
[JMAG Newsletter 2011年夏号より]