※ライセンス管理者に案内をしているライセンスIDとパスワード、もしくはユーザーIDをご用意ください。
※尚、JMAG WEB MEMBER(無料会員)向けのサービスとは異なります。ご注意ください。
概要
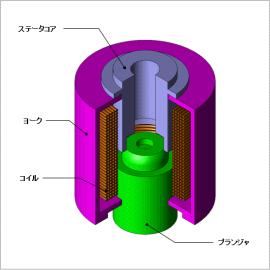
電磁弁は、鉄心を並進運動させて液体や気体の流入出量を調整するために用いられます。コイルに電流を通電すると電磁石が形成され、可動部と固定部との間に電磁吸引力が発生します。弁の開閉には高い応答性が求められるため、駆動に用いる電源や電磁弁が、要求される応答性や吸引力を満たすか否かは重要な評価項目となります。
電磁弁が良好に機能するためには、制御信号に対して応答性を向上させる必要があります。そのためには、可動子の上昇時間を短くする必要があります。しかし、電磁弁のレイアウトの自由度を高められるため、電磁弁の体積は最小限に抑えたいという要求があります。これらの条件を満たすため、FEAの最適化機能を用いた自動計算を適用すると工数を大きく削減することができます。
ここでは、多目的最適化アルゴリズムを用いて電磁弁の形状を最適化した事例を紹介します。
電磁弁が良好に機能するためには、制御信号に対して応答性を向上させる必要があります。そのためには、可動子の上昇時間を短くする必要があります。しかし、電磁弁のレイアウトの自由度を高められるため、電磁弁の体積は最小限に抑えたいという要求があります。これらの条件を満たすため、FEAの最適化機能を用いた自動計算を適用すると工数を大きく削減することができます。
ここでは、多目的最適化アルゴリズムを用いて電磁弁の形状を最適化した事例を紹介します。
最適化条件
可動子の上昇時間は、コイルに通電されてから可動子が最終位置に達するまでの時間を測定します。したがって、可動子形状が上昇時間へ与える影響に着目します。
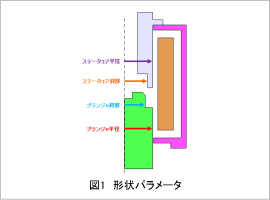
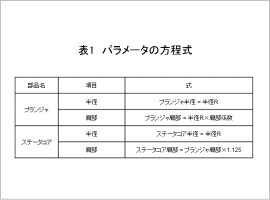
変数とする形状パラメータを図1に示します。最適化するための形状パラメータは、半径と肩部係数の2つのパラメータで表現できます。形状パラメータの関係を示したパラメータの方程式を表1に示します。
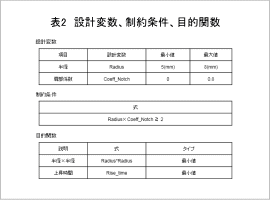
この事例では、可動子の上昇時間が短い場合には体積が大きくなり、体積が小さい場合には可動子の上昇時間が長くなるトレードオフの関係があります。上昇時間を短く、かつ、体積を最小化するような最適形状を求めます。最適化の設計変数、制約条件、目的関数を表2に示します。
上昇時間と体積
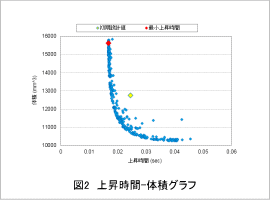
図2に上昇時間 – 体積のグラフを示します。なお、時刻0.06(sec)までにプランジャが駆動範囲の上限(最終位置)に達することが前提となっており、この前提を満たしていないものを除外しています。
半径すなわち体積を大きくすると可動子が最終位置に達する時間が短縮されることがわかります。最小上昇時間は16.8(msec)で、その時の半径は7.9(mm)、体積は15,621(mm^3) となります。
初期設計値のケースを黄色、最小上昇時間のケースを赤色のマーカーで示します。最小上昇時間のケースと初期設計のケースを比較すると、最小上昇時間のケースは上昇時間が32(%)減少しますが、体積が23(%) 増加しています。
半径すなわち体積を大きくすると可動子が最終位置に達する時間が短縮されることがわかります。最小上昇時間は16.8(msec)で、その時の半径は7.9(mm)、体積は15,621(mm^3) となります。
初期設計値のケースを黄色、最小上昇時間のケースを赤色のマーカーで示します。最小上昇時間のケースと初期設計のケースを比較すると、最小上昇時間のケースは上昇時間が32(%)減少しますが、体積が23(%) 増加しています。
半径と体積上昇時間
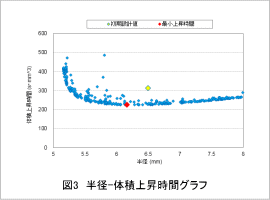
上昇時間と体積との間の最適値を見つけるために、体積上昇時間(体積×上昇時間)で評価します。半径と体積上昇時間のグラフを図3に示します。なお、時刻0.06(sec)までにプランジャが駆動範囲の上限(最終位置)に達することが前提となっており、この前提を満たしていないものを除外しています。
初期設計値のケースを黄色、最小上昇時間のケースを赤色のマーカーで示します。 図3に示されているとおり、最適値は体積上昇時間224(s・mm^3)と半径6.16(mm)で あることがわかります。この条件では、初期設計から体積は5(%)減少し体積上昇時間は28(%)減少 します。これは体積に対する上昇時間が改善することを示しています。
初期設計値のケースを黄色、最小上昇時間のケースを赤色のマーカーで示します。 図3に示されているとおり、最適値は体積上昇時間224(s・mm^3)と半径6.16(mm)で あることがわかります。この条件では、初期設計から体積は5(%)減少し体積上昇時間は28(%)減少 します。これは体積に対する上昇時間が改善することを示しています。


