※ライセンス管理者に案内をしているライセンスIDとパスワード、もしくはユーザーIDをご用意ください。
※尚、JMAG WEB MEMBER(無料会員)向けのサービスとは異なります。ご注意ください。
概要
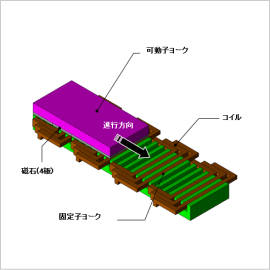
リニアモータは、高加減速、高い位置決め精度を実現することができるため、搬送装置や工作機械の駆動装置などに使われています。性能向上の課題として、応答性を向上するためには大きな推力を得ることが求められますが、一方で、推力変動や吸引力を低減したいというトレードオフの要求も満たす必要があります。
大きな推力を得るためには材料の非線形磁化特性や磁石の減磁特性と考慮する必要があり、推力変動を評価するためには、詳細な形状をモデル化した上で解析する必要があるため、有限要素法に基づく磁界解析シミュレーションによって検討する必要があります。
ここでは、推力変動の要因となるコギングを求め、駆動時の推力および吸引力を評価します。
大きな推力を得るためには材料の非線形磁化特性や磁石の減磁特性と考慮する必要があり、推力変動を評価するためには、詳細な形状をモデル化した上で解析する必要があるため、有限要素法に基づく磁界解析シミュレーションによって検討する必要があります。
ここでは、推力変動の要因となるコギングを求め、駆動時の推力および吸引力を評価します。
コギングリップル
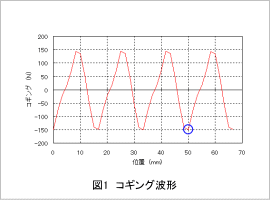
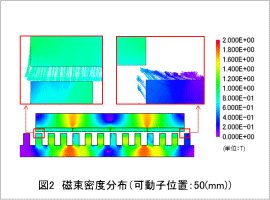
コギング波形を図1に示します。また、コギングの要因を考察するために、図1の丸で囲まれた場所(タイミング)での磁束密度分布を図2に示します。
図2で可動子の端部を見ると磁束密度分布に偏りが見られ、その磁気回路的なアンバランスがコギングリップルを大きくする要因になります。
推力/吸引力
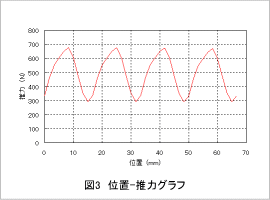
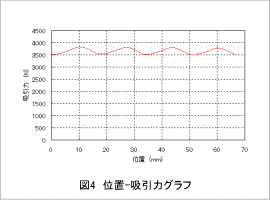
図3に位置-推力特性、図4に位置-吸引力特性を示します。
推力/吸引力の周期はそれぞれ、コギングの周期と同じことがわかります。コギングリップルは推力変動に影響するため、推力変動を小さくするためにはコギングリップルを小さくする必要があります。また、吸引力は回転機におけるラジアル力と同じでギャップ部の磁束の流れの影響を受けるため、低減するにはスロット形状の変更などによりギャップ間を垂直に流れる磁束を減らすことが考えられます。