モータ設計講座
この連載ではモータの設計の初心者を対象として、初歩的な知識の習得を望む方に設計の情報を提供することをテーマとして、我々が考えるモータ設計の進め方を紹介しております。 前回は初期設計を行い、詳細設計のスタート地点となる初期設計案をまとめました。最終回となる第3回では、設計の仕上げとなる詳細設計に取り組みます。
詳細設計のキーワードはトレードオフで、JMAG-Designer/JMAG-Expressが得意とする分野です。JMAG-Designer/JMAG-Expressを使って試行錯誤した事例を御紹介することで、モータの詳細設計の進め方のヒントになればと考えています。
モータの詳細設計
初期設計を行い、要件を満たせることを確認したら、モータの詳細設計に取りかかります。ここからがモータ設計者にとって本番です。”詳細設計”は言い換えると”最終設計”なので、全てを決めます。部品の価格や作り方まで文字通り全てです。そうでなければ実機を作ることができません。部品図までは書かないにしても、その寸前までを設計者はイメージできている必要があります。モータ設計者は、実際にモータ部品を実際の機械に取り付ける設計者やモータを組み立てる技術者の疑問に応える必要があります。モータ設計者の他にはその疑問に応えられる人は居ません。”ここの寸法は0.5mmでなければいけないのか?作りにくいから、0.6mmにしたい”という提案に対しても、信念に基づいて”0.5mmで御願いします。理由はカクカクシカジカ…”と説明できなければいけません。この状況は別にモータ設計に限ったことではありません。我々のソフトウェアの開発もそうですし、ラーメン屋さんが新しいメニューを考案するときの苦労も同じです。最後の産みの苦しみが一番大変です。
またまた、前置きが長くなってしまいましたが、詳細設計におけるキーワードは以下となります。
- 無駄をそぎ落とす
- トレードオフを吟味し高次元でバランスさせる
- 品質を向上する
- 信頼性は十分確保する
正確にはそれぞれは独立した事象ではありませんが、このテーマに沿って詳細検討を進め、設計案を煮詰めていくことで良い製品に近づけていけるはずです。
第3回では、これらのテーマに沿ってJMAG-Express PublicやJMAG-Designerを使用した典型的な検討例を示しながら、モータの詳細設計を進めてみたいと思います。初期設計案として第2回でまとめたものを記します(表1)。
表1 初期検討で決定した諸元
無駄をそぎ落としていく
まずは無駄をそぎ落としていきます。わかりやすい無駄の例は、磁束密度がやたらに低い磁路です。この部分をなくせば軽量化できます。あるいは、コイルの通路に振り分ければ銅損を減らせる可能性もあります。ただ、実際には無条件な無駄はあまり残っていない場合が多く、結果的には余裕を削って行くトレードオフの問題になる場合が多いです。
見落とされやすい無駄な磁路としてはロータ内側の磁路が挙げられます。シャフトとの勘合する必要もあるので、磁気回路の都合で無闇に削るわけにはいきませんが、検討する価値はあります。まずは磁路として必要最低限なスペースを確認します(図1)。
シャフト径は初期設計案では16(mm)にしていましたが、これを±8(mm)の範囲で振ってみました。シャフト径を太くするということは、ロータの磁路を狭めることに相当します。
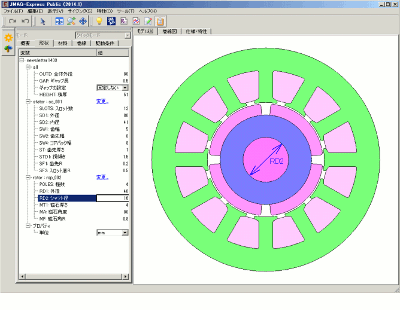 図1 シャフト径の検討
図1 シャフト径の検討
シャフト径の違いによるロータ重量とトルク定数の相関関係、シャフト径の違いによる回転数-トルク特性をみてみます(図2、3)。シャフト径(穴径)を振った結果、初期値の16(mm)より細くしてもトルク定数の向上はありませんでした。これは磁石内側の磁気抵抗が初期値でも十分低く、磁路を増やしても重量が増えるだけの無駄であることがわかりました。逆に太くした場合、20(mm)では殆ど影響が見えませんが、24(mm)まで太くすると磁石内側の磁路が足りなくなって、トルク定数が低下しています。
したがって、シャフト穴径は16(mm)から20(mm)に太くしても差し支えないことが解ります。ちなみにロータコア重量は235(g)が191(g)に軽減されるので、40(g)の軽量化となります。全体で2(kg)程度のモータなので、寄与度としては小さいかなと言うのが印象はありますが、無駄は無駄ですので、20(mm)に変更することにします。
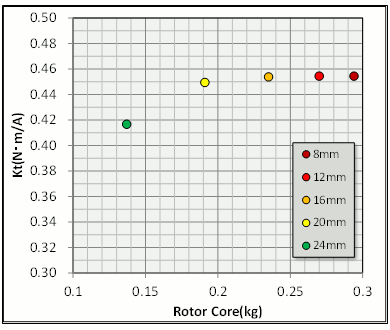 図2 シャフト径によるロータ重量とトルク定数の関係
図2 シャフト径によるロータ重量とトルク定数の関係
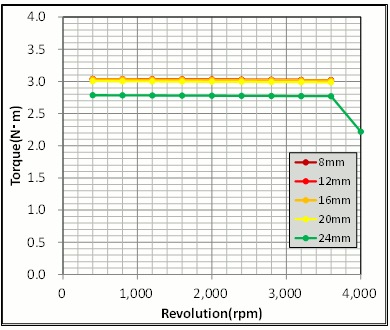 図3 シャフト径の違いによる回転数-トルク特性
図3 シャフト径の違いによる回転数-トルク特性
トレードオフを吟味する
設計の醍醐味はトレードオフです。あちらを立てるとこちら立たずというわけで、明らかに矛盾している設計パラメータを、なんとかまとめ上げるのが設計者の仕事です。
ここでは、ステータコアのヨークの幅について検討しました。外径と積厚を固定すれば、全体の外径・重量への影響はほとんどありません。モータ内部のスペースをうまくバランスさせるかがモータ設計者の検討項目になります。コアバックを厚くすると磁気飽和のリスクは減りますが、コイルの巻線スペースは圧迫され、抵抗値が増加し、銅損が増加します。コアバックを薄くした場合はその逆です。銅損を適切に抑えつつ、磁気飽和させないための寸法検討になり、とまさにトレードオフ、調整、すり合せになります。
コアバックの初期値は8(mm)で、±2(mm)変更して検討しました(図4)。その際、コイルの巻数60(turn)および、占積率50.4(%)を維持するように素線径を変化させ、相抵抗のみが連動するようにしました。パラメータを示します(表2)。
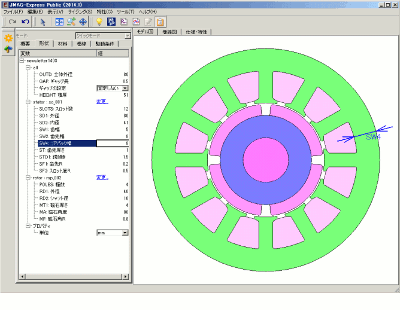 図4 コアバック幅の検討
図4 コアバック幅の検討
表2 コアバック幅と素線径、相抵抗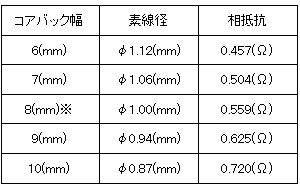
コアバック幅を変えた場合の相抵抗とトルク定数の相関関係を確認すると、初期値の8(mm)より増やしても、トルク定数が変化しないことから、初期値でも磁気回路的には余裕があることがわかります(図5)。しかし、相抵抗はスロット面積が減ることにより線形に増加していますので、コアバック幅を8(mm)より拡げることにメリットがないことがわかります。逆に狭めた場合は、狭めるにしたがってトルク定数が低下しており、磁気回路に影響が出始めていることが解ります。相抵抗に関しては線形に低下していることも確認できます。
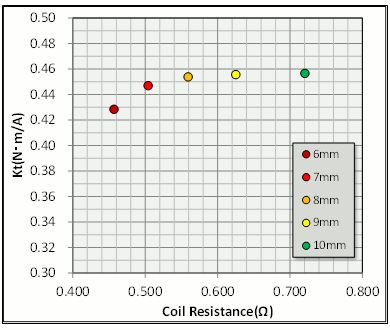 図5 コアバック幅による相抵抗とトルク定数の関係
図5 コアバック幅による相抵抗とトルク定数の関係
コアバック幅の違いによる回転数-トルク特性を確認すると、7~10(mm)ではあまり特性に影響は出ていませんが、6(mm)から最大トルクが低下している様子が確認できます(図6)。
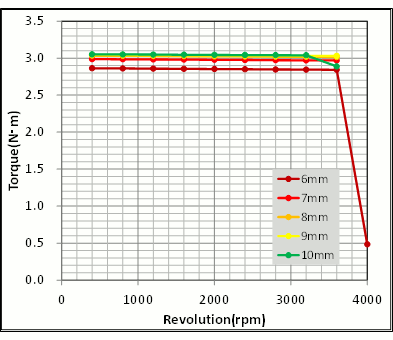 図6 コアバック幅の違いによる回転数-トルク特性
図6 コアバック幅の違いによる回転数-トルク特性
回転数-効率特性を確認すると、コアバック幅を狭めることで相抵抗が低下するので効率が向上していますが、7(mm)より狭めても殆ど差がないことがわかります(図7)。これらを総合し、コアバック幅は7(mm)に変更することとします。
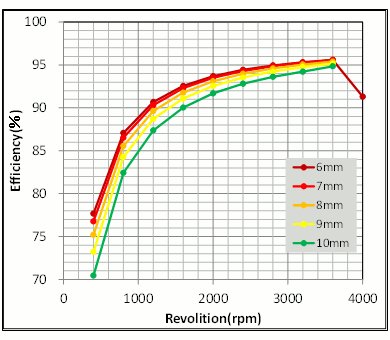 図7 コアバック幅の違いによる回転数-トルク特性
図7 コアバック幅の違いによる回転数-トルク特性
次に歯幅について検討します。磁気回路での位置付けとしてはコアバック幅と同じで、歯幅を狭くすることでコイルの面積を拡げることが可能となり、相抵抗の低減が期待できますが、磁気飽和のリスクが高まります。したがって、相抵抗と磁気飽和のバランスを取ることが検討方針となります。初期設計案では歯幅は5(mm)でしたが、±2(mm)の範囲で振ってみました(図8)。
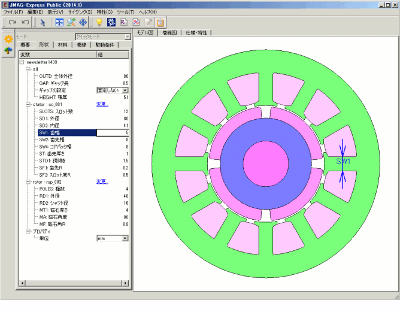 図8 歯幅の検討
図8 歯幅の検討
歯幅を変えた場合の相抵抗とトルク定数の相関関係を見ると、歯幅を変えることにより、相抵抗と磁気抵抗がトレードオフの関係になっていることがよくわかります(図9)。歯幅を4(mm)から3(mm)に狭めると急激に磁気飽和が進み、トルク定数が低下しています。一方、6(mm)と7(mm)ではトルク定数に変化がありませんので、磁気回路として余裕があることがわかります。ティースの平均磁束密度を確認しても、4(mm)で1.8(T)に達しており、ケイ素鋼板の一般的な飽和磁束密度の2(T)に近づいていることがわかります(表3)。
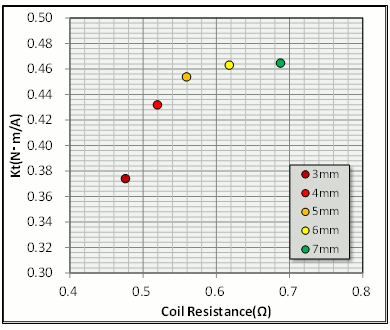 図9 歯幅による相抵抗とトルク定数の関係
図9 歯幅による相抵抗とトルク定数の関係
表3 歯幅と平均磁束密度(ティース)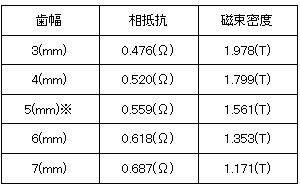
歯幅を変えた場合の回転数-トルク特性をみると、既に5(mm)以上ではトルク定数が変化していないことから解っているように、最大トルクに変化は殆どありません(図10)。しかし、4(mm)、3(mm)と狭めると最大トルクが低下していることが解ります。
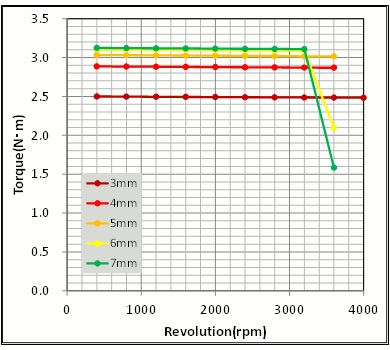 図10 コアバック幅の違いによる回転数-トルク特性
図10 コアバック幅の違いによる回転数-トルク特性
トルク定数の低下は誘起電圧定数の低下と等価のため、高回転域での出力特性が向上していると捉えることで、設計的にメリットがあるように感じることもあるかと思いますが、高回転化を目指すのであれば、コイル巻数を減らしたり、磁石量を減らしたりすることで、高回転化を実現した方が正しいアプローチです。折角の磁石磁束を、ティースを細くしてスポイルするのは得策ではありません。
次に磁石の厚さについて確認してみましょう。特に希土類磁石の場合、モータの他の部品に比べて材料費が非常に高いので、使用する量について吟味が必要であることは言うまでもありません。
磁石の厚みを増すことで磁石自身の起磁力は増加します。しかし、磁石の比透磁率はほぼ1.0のため、モータの磁気回路で考えると厚みを増やした分だけエアギャップが伸びたのと同様の効果になってしまい、磁気回路全体での磁気抵抗が増加するので、厚みの増加分ほど磁束量は増えません。初期設計案は4(mm)ですが±2(mm)の範囲で検討してみました(図11)。
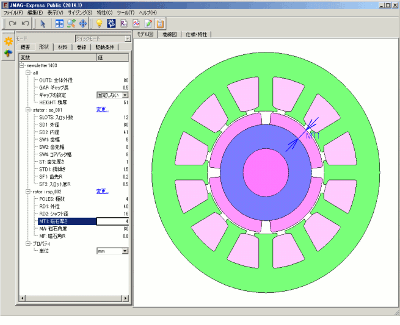 図11 磁石厚さの検討
図11 磁石厚さの検討
磁石厚さによる磁石重量とトルク定数の関係を見てみます(図12)。磁石を初期値よりも厚くしてもトルク定数はあまり増加していません。これは、前述の通り起磁力と磁気抵抗の増加によるものです。一方、薄くしていくとトルク定数の大きく低下しています。モータの磁気回路では磁石以外にも、ロータとステータの間にエアギャップが存在しています。磁石を薄くしていくと、この変化しないエアギャップ長が相対的に効いてくるため、磁石を薄くする方がトルク定数への影響が大きい様子が確認できます。回転数-トルク特性を確認すると、トルク定数の変化が出力特性にそのまま表れている様子が見てとれます(図13)。
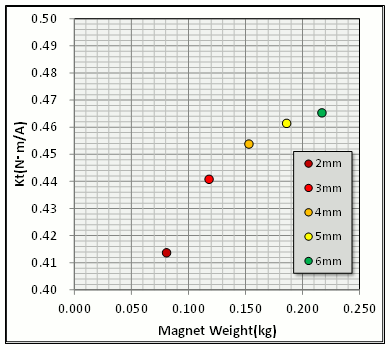 図12 磁石厚さによる磁石重量とトルク定数の関係
図12 磁石厚さによる磁石重量とトルク定数の関係
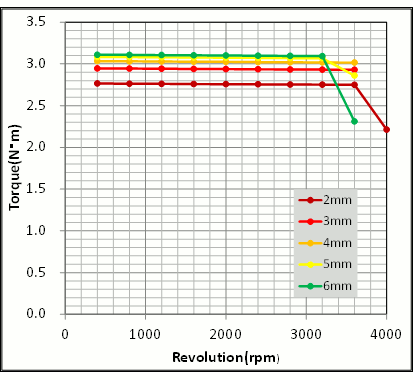 図13 磁石厚さの違いによる回転数-トルク特性
図13 磁石厚さの違いによる回転数-トルク特性
磁石の厚みと回転数-トルク特性の関係を確認した結果、初期設計の4(mm)から3(mm)に薄くしても良さそうなことが確認できました。ただし、実際に厚みを決定する場合には、反磁界減磁や熱減磁を考慮する必要があります。この様な解析は計算精度が必要になるので、JMAG-Designerのような精度の高いソフトウェアを用いて判断するのがよいと思います。
本来のモータ設計であれば他にもトレードオフを色々検討すべきことがありますが、このまま全てについて実施すると一冊の本になってしまうので、トレードオフに関する事例の提示はこの程度に止めさせていただき、次のテーマである品質の向上についての検討してみたいと思います。
品質を向上する
品質とは何を指すか判断が分かれるところですが、ここではコギングトルク等のトルク変動や振動の要因を低減することが品質向上に繋がるモノとします。
例えばコギングトルクのように形状に対して敏感な検討はJMAG-Designerで行います。ここでは、磁極の弧の角度をパラメータにしてコギングトルクがどの様に変化するのかを確認して見ました。JMAG-Designerの解析画面は、汎用目的である分、設定項目や結果分析も多岐にわたり、高精度な解析を行うことができます(図14)。
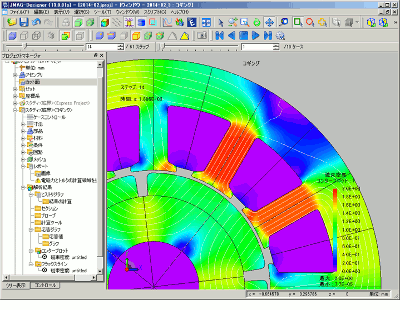 図14 磁石角度の検討
図14 磁石角度の検討
得られたコギングトルクの波形を分析していきます(図15)。初期設計案は磁極の弧の角度は80(deg)で極間に10(deg)分の隙間を空けています。このときのコギングトルクは±0.65(N・m)でした。磁石の角度を狭めて隙間を拡げるとコギングトルクが低下していき、68(deg)まで狭めると±0.15(N・m)まで低下する様子が確認できました。しかし、それ以上狭めると、逆にトルク変動が増加しました。
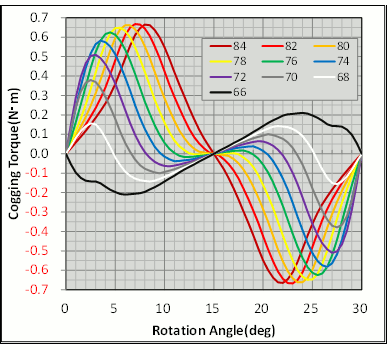 図15 コギングトルク波形
図15 コギングトルク波形
コギングトルク低減のために磁石の角度を狭めると、当然磁石磁束が低下しますので、トルク定数の低下に繋がります。このときの誘起電圧波形(図16)をJMAG-Designerで求めてみます。回転数は600(rpm)です。
まず特徴的なのは、誘起電圧波形の振幅は概ね14(V)付近で大きな差はありません。波形は、磁石の弧の角度が大きい方が矩形波に近く、角度が小さくなるにしたがって高次成分が増えているように見えます。特にコギングトルクが最小となった68(deg)では最大が15.5(V)まで増加し、60(deg)での落ち込みは12(V)を下回っています。このように誘起電圧が激しく変化すると、電流を正弦波に保つのが難しく、鉄損が増加する要因になるので、注意が必要となります。
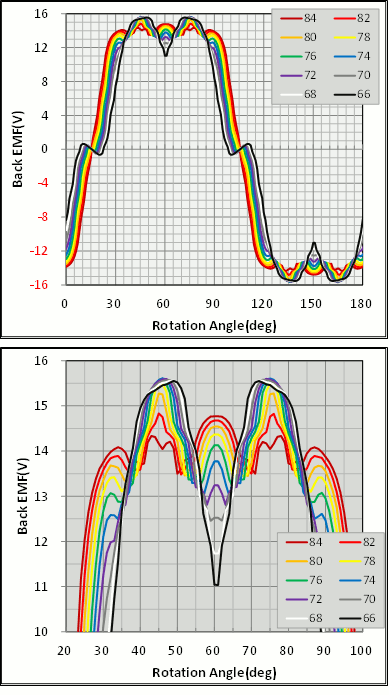 図16 誘起電圧波形 上;1周期分、下ピーク付近
図16 誘起電圧波形 上;1周期分、下ピーク付近
誘起電圧波形をFFT処理した結果で分析してみます(図17)。磁石角度は84(deg)から66(deg)まで変化させているので、単純換算で磁束数は78(%)まで低下させていることになります。基本波である20(Hz)の電圧振幅は角度を狭めるにしたがって漸減しますが17.5(V)が15.8(V)に低下しているだけなので、91(%)に留まっています。一方、スロット高調波にあたる60(Hz)成分は4.6(V)が0.6(V)まで低下しており、14(%)と大幅に低減しました。しかし、回転5次の100(Hz)成分は一旦低下した後に急上昇するという動きを示しており、結局1.8(V)から3.3(V)に倍増していました。このように、モータは基本波だけでは読み切れない次数ごとの性質を持っているので、最終的な判断を下すためには精度の高いツールを使う必要があると考えています。
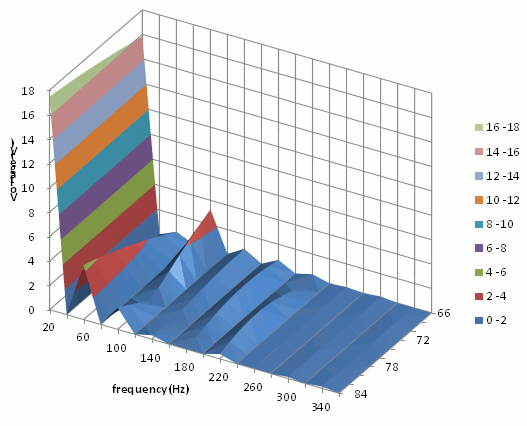 図17 磁石角度ごとの誘起電圧のスペクトル比較
図17 磁石角度ごとの誘起電圧のスペクトル比較
信頼性は十分か
性能を確保し、品質を向上したら、最後は信頼性です。電磁機械ですから出力が出るのは当然ですが、世の中の役に立つためには、振動や衝撃が加わっても壊れないであるとか、色々な環境において安定した性能を発揮するなどの信頼性が必要となります。これらは初期検討や詳細設計の中である程度片がついているべきです。勿論、壊れることは問題外ですが、余裕がありすぎる場合も設計的には問題であると思います。
ここでは温度範囲内で特性がどの様に変わるかを確認して見ましょう。今、この原稿は2月に書いています。この間ニュースで北海道での内陸で-30(℃)を下回ったというニュースがありました。一方、昨夏は四国で40(℃)を超えたことが話題になりました。狭い日本でも-30~+40(℃)の温度変化するわけですから住んでいる人間も大変ですが、モータもその範囲でキチンと機能することが必要です。ここでは20(℃)±40(℃)で性能がどのように変わるかを確認します。
モータ部品で温度の影響を強く受けるのが、磁石とコイルです。ネオジム焼結磁石の残留磁束密度(Br)の温度係数は-0.11(%/K)といわれているので、±40(℃)変化するとBrが±4.4%変化することがわかります。同様にコイルの電気伝導率の温度係数は0.38(%/K)といわれているので±40(℃)変化すると±15.2%変化することがわかります。
この影響をモータに適用して、温度の違いによってトルク定数とコイル抵抗値がどの様に変化するかを示します(図18)。初期温度を20(℃)とし、60(℃)まで上昇させるとコイルの抵抗値が上昇して損失が増加し、磁石が弱まってトルク定数が低下するという相乗効果で出力・効率が低下してしまいます。磁石の強さで決まるトルク定数に影響が出ますが、温度係数が大きい銅損の変化が大きくなっていることがわかります。逆に、温度を-20(℃)まで下げるとBrは上昇し、抵抗も下がるので、特性が向上することが期待できます。
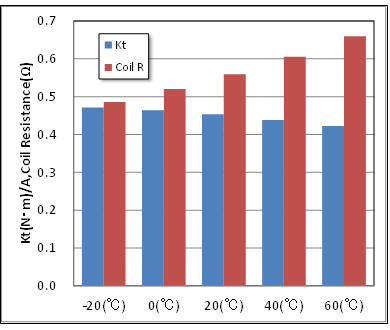 図18 温度の違いによるトルク定数、コイル抵抗の変化
図18 温度の違いによるトルク定数、コイル抵抗の変化
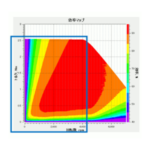
次に、実際にモータ特性にどれほどの影響があるのかを確認して見ましょう。回転数-トルク特性をみると、トルク定数が低下しているため最大電流時のトルクが低下している様子が確認できます(図19)。一方、磁石磁界が弱まっている分、誘起電圧定数も下がるので高回転まで回るようになります。回転数-効率特性では、温度の上昇により銅損が増加するので効率が低下している様子が確認できます(図20)。特に出力中で銅損が支配的となる低回転で効率が低下し、20(℃)で75(%)あった効率が60(℃)で70(%)まで低下することがわかります。
この影響は、実運用状態では自分自身の発熱にでてきます。モータの出力を一定に維持しようとした場合、温度が上昇していくと、モータ温度が上がる→性能・効率が低下→入力を増やして回復→発熱量の増加→モータの温度が更に上がる→…の連鎖反応に陥り、急激に温度が上昇することもあります。特に高温時に目標効率以上(=目標損失以下)の性能を発揮できているかを確認することが重要になってきます。
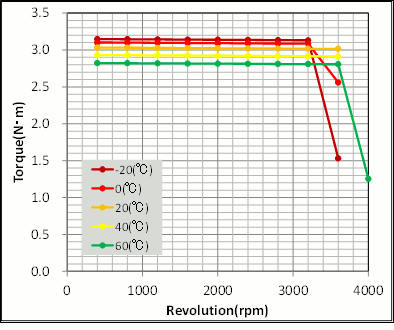 図19 温度の違いによる回転数-トルク特性
図19 温度の違いによる回転数-トルク特性
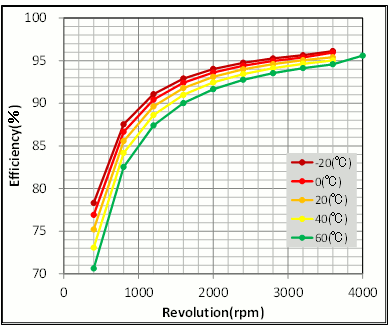 図20 温度の違いによる回転数-効率特性
図20 温度の違いによる回転数-効率特性
ゴールに辿り着けたか
これらの詳細検討により設計案がブラッシュアップされました。無事要件を満たし、信頼性やコストの見通しがたったでしょうか。そうであれば、設計も完了です。
今回の数少ない検討の中でも初期設計案に対して各部の見直しを図りました。変更点に示します(表4)。検討の結果、若干の改善を図ることができました。特に磁石のサイズを削減できたことは、コスト面で有利になります。
表4 初期設計案と最終案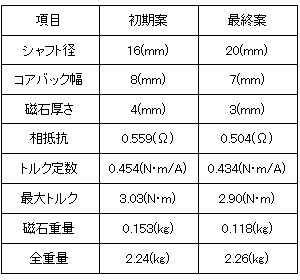
回転数-トルク特性、回転数-効率特性を見ると、最終案では最大トルクは3.03(N)から2.90(N・m)に下がりましたが、効率は若干改善しています。その上で、磁石を20(%)以上低減できているので悪くない結果だと思われます(図21、22)。
もちろん、誌面の関係で一部しか検討していませんので、実際の設計では、もっと様々な検討を行う必要はあります。一つの検討で何割も改善することはないと思います。せいぜい1(%)くらいでしょう。しかし、”塵も積もれば山となる”の諺どおり、多数の項目で1(%)ずつでも改善すれば、製品では数(%)以上の改善することが期待できるので、地道な努力を続けることは大切です。
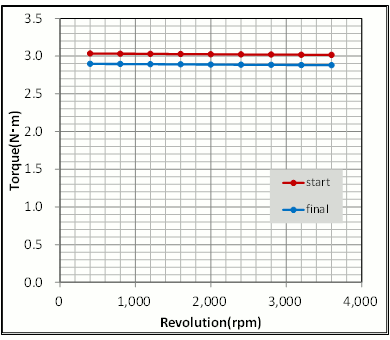 図21 初期設計案と最終案の回転数-トルク特性
図21 初期設計案と最終案の回転数-トルク特性
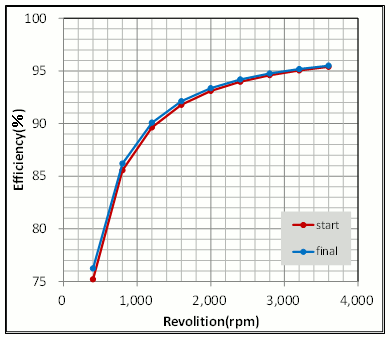 図22 初期設計案と最終案の回転数-効率特性
図22 初期設計案と最終案の回転数-効率特性
試作機からのフィードバックを活かす
詳細設計が終わり、無事の設計がまとまれば試作に移ることになり、答え合わせになります。ここで色々なことがおきますので、更に対策していきます。解りやすく、設計(解析)ではトルクが○○(N・m)出るという計算結果だったが、実機では××(N・m)に留まったということもあるかと思います。その原因を探り、とにかく対策するしかないのですが、その過程で、どの時点の検討・どの部位で誤差が生じたのかを把握するチャンスとなり、非常に重要なフィードバックが得られます。そこを把握し、検討方法を修正することで次回設計時における改善点が明確になります。ベテランの設計者はそのような経験を沢山持っているのです。予め性能マージンを数%持っておいて、最後に吐き出すとか、材料にファクターを掛けて検討をしていくなどのノウハウがあると思います。
連載のおわりに
今回の連載では、私たちなりに考えるモータ設計のプロセスをまとめてみました。モータ設計にこれから取り組む方や興味をお持ちの方には設計の流れをイメージしていただけたと思います。また、設計の流れの中でJMAG-Express PublicやJMAG-Designerのツールを活用していく方法などもご理解いただけたのではないでしょうか。
ただし、設計におけるツールの寄与度は所詮気の利いた電卓程度です。良い設計をするためには、設計者のセンスが重要である必要なことは間違いありません。ツールは設計者の判断を助けることはあっても、ツール自身は主体的に良い設計案を生み出したりはしません。多分、最適化ソフトウェアと磁界解析ソフトを組み合わせて出てくる最適設計案は、ベテラン設計者が手計算でひねり出してきた設計案に適わないと思います。それに、ベテラン設計者が最適化ソフトと磁界解析を組み合わせれば更に最強の設計案を生み出すことが期待されますので、どんな道具を使っても初心者はベテランには適わないのです。したがって、とにかく設計初心者は場数を踏んでセンスを磨いていただき、ベテランス設計者になっていただくしか道はないのです。その練習台としてJMAG-Express PublicやJMAG-Designerを使って設計を進めてください。
(坂下 善行)
コラム トルク変動発生の様子
モータ設計講座ではモータ設計の流れを中心に解説していますが、このコラムでは設計講座で説明しきれなかった話題についてJMAGを使った簡単な実験を行いながら考えてみます。
今回の話題はトルクリップルについてです。モータ設計者にとってトルク変動の低減は課題であり続けるテーマだと思います。残念ながら、我々はここでトルク変動低減の妙案や秘策を披露するほどの設計力を持っていませんので、JMAGを使ってトルク変動の様子を示す事で、皆さんがトルク変動低減を対策される際のヒントを提示できればと考えています。
そもそも、モータはどの様にトルクを発生しているのでしょうか。みなさんはトルク(電磁力)を見た事がありますか?私はありません。教科書を見ると、ローレンツ力によってトルクを生じるとか、マックスウェル応力により発生する等それらしいことが説明されていますが、本の中の話です。私は実際にトルクが出ている様子を見たいと常々思っていました。その思いは未だ果たされていないのですが、JMAGはそれに近いもの見る機会を与えてくれます。
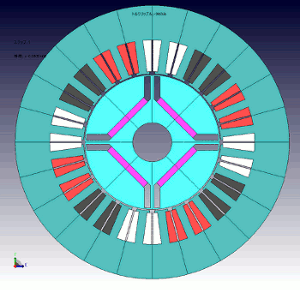 図1 モータモデル形状
図1 モータモデル形状
トルク変動発生の様子を観測するためにIPMモータについて解析を実行しました(図1)。対象は4極24スロットですので、電気角は90(deg)になります。電流は三相正弦波を通電したところ、トルク波形は図の通りになりました(図2)。トルク波形のグラフを見ると、トルク変動が15(deg)ごとに大きく落ち込んでおり、スロットピッチによる影響である事が予想されます。ここで、”スロットピッチによる影響である事が予想されます”と軽く結論づけて解った気になると、トルクリップルが見えてきません。もう少し掘り下げる必要があります。
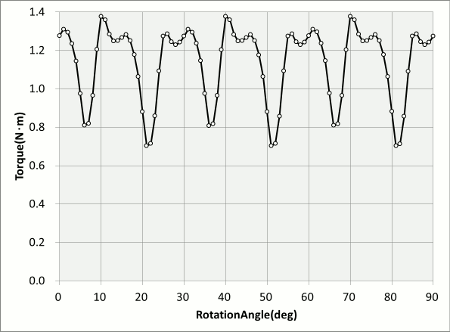 図2 モータのトルク変動
図2 モータのトルク変動
普通にトルクを発生している状態のモータの磁束線と節点力を確認してみます(図3、4)。特徴的なのは、とにかくロータとステータの吸引力(半径方向の力)が非常に大きいということです。ただし半径方向の力はトルクに寄与しないので、ここでは無視します。
ティースから出ている電磁力ベクトルを見ると、ロータのN極とS極の境目付近のティースでトルクに繋がるθ方向の大きな力が出ている事がわかります。他の位置にあるティースには、有効なトルクは出て無さそうです。
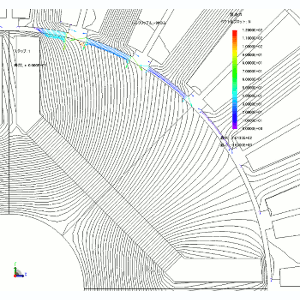 図3 モータ内の磁束線と節点力ベクトル
図3 モータ内の磁束線と節点力ベクトル
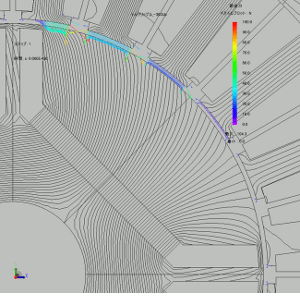 図4 モータ内の磁束線と節点力ベクトル(拡大)
図4 モータ内の磁束線と節点力ベクトル(拡大)
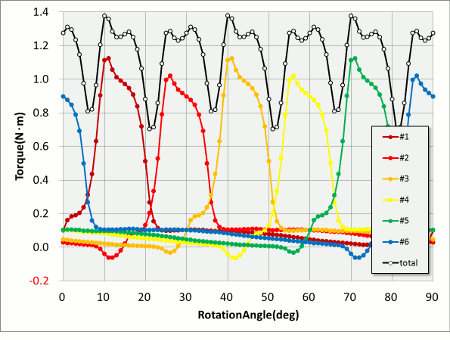 図5 各ティースの全体のトルク波形(電気角1/2周期分)
図5 各ティースの全体のトルク波形(電気角1/2周期分)
節点力ベクトルの絵から何となく推測できていましたが、実際にグラフにしてみるとなかなか壮観です。これにより解ることは、モータが発生するトルクの大部分は一本のティースで生じている事がわかります。回転に伴い、その歯が入れ替わることでトルクを連続して発生していることも良くわかります。1本のティースに着目すると、電気角半周期である90(deg)のうち15(deg)弱の間トルクを発生し、残りの75(deg)強の間はお休みしている感じになっています。ここで、”15(deg)弱”といったのが重要で、トルク変動はこの”弱”が大きく、オーバーラップが上手くないときに谷ができることで発生していることが解ります。
もう少しトルク波形を細かく見て見ましょう。1ティースピッチに相当する0-15(deg)の区間で拡大してみます(図6)。
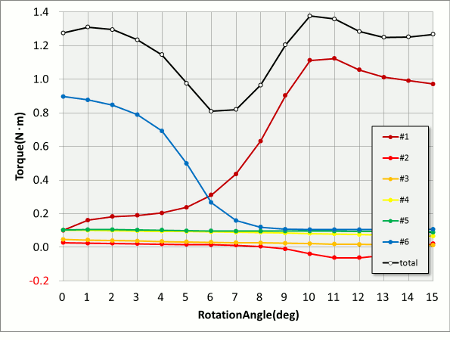 図6 各ティースの全体のトルク波形(1スロット分)
図6 各ティースの全体のトルク波形(1スロット分)
トルク変動を低減するためには、オーバーラップが上手くいくようにすれば良いという結論が導かれるのは言うまでもありません。山の時間を増やすようにできれば良いのですが、実際には山を切り崩して谷を埋めるイメージで対策していくことになると思います.この辺の対策は、スロットやロータの詳細形状などの実際の幾何形状が影響してくるので、JMAG-Designerのような高精度な電磁界有限要素解析(Finite Element Analysis:FEA)を利用しないと検討することすれできないと思います。
今回はIPMモータについて試してみましたが、SPMでどうなるのか、集中巻(分数スロット)の場合はどうか、でも様子が変わってくると思われます。誘導電動機でどうなるのかなども興味は尽きません。我々はどうすれば上手くいくかは解りません。設計者の腕の見せ所ですので、JMAGを活用していただき、設計者の皆さんに解決していただくことを期待しております。
[JMAG Newsletter 2014年3月号より]