モータ設計講座
連載第1回目ではモータ設計講座を始めるに至った経緯を御説明させていただきました。第2回ではいよいよモータ設計に取り込んでみたいと思います。今回のテーマは、設計の足掛かりとなる概念設計についてです。恥ずかしながら、我々なりに学んだ成果を披露させていただきますので、暖かく見守っていただきつつ、皆様の業務の参考になれば幸甚です。
モータの概念設計
モータの設計を始めるに当たり、まずは「なぜ設計する事になったのか」の経緯をハッキリさせる必要があります。開発をスタートさせた何らかの目的があるはずです。この目的を明確にする事こそ、その後の方向性を正しく定義づけることになります。
従来品をベースとしてバリエーションを設計する場合や、欠点を改善する場合は従来品がスタート地点になります。全くの新規設計の場合も、類似の性能や性格を持つ従来製品をお手本にするのが一般的です。従来品は様々な検討により導き出された結論の結集で、且つ実戦での評価を受けていますから、課題があるにせよ信頼と実績を持っています。従来品を肯定して盲信しろと言っているのではなく、現状の設計を再評価する事は、設計を進めるために重要だと申し上げたいだけです。
理屈っぽい話はこれくらいにして具体的な検討に移りたいと思います。モータの概念設計の流れを簡単にまとめると図1のようになります。
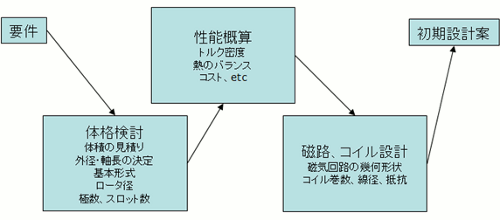 図1 モータ設計の流れ
図1 モータ設計の流れ
要件をスタート地点として、大まかな体格を決め、次に経験値などに基づき出力やトルク、熱の妥当性などの性能を確認します。最後に磁気回路の幾何形状やコイルの線径などを決め、初期設計案としてまとめます。この初期設計案が詳細設計の叩き台になります。
まず体格を決める
モータに限らず、モノには適当なサイズというものがあります。情報処理機器でもスマホのように手のひらに収まるようなものから、スーパーコンピュータのように建物いっぱいでも納まらないものまでありますが、その大きさは性能という能力により決まります。もちろん、芸術作品のように価値が重要で物理量では量れないものも世の中に存在しますが、大体の機械のサイズ(体格)はそれが為す仕事により概ね決まります。言い換えると、単位体積・重量あたりにこなせる”仕事”の密度が一定になると言うことです。モータの場合、小さいモータは出力が小さく、大きな出力を出すモータは大きくなると言うことです。
重量が大きなものは体積も大きくなるので、熱容量や放熱面積が大きくなり、大出力が可能になります。この辺の考え方は改めていうほどの事ではありませんが、意外にキチンと認識出来てない場合が多いので、ここで確認させていただきました。
従来品のモータをおさらいすると、重量出力密度にある程度の相場値があることが分ります。大体0.3~1.0(kW/kg)あたりが目安となっています。出力密度を低めに設定する場合、余裕を持たせていると考える事ができます。昼夜稼動の工場のラインで使うようなモータや新幹線の駆動モータのように連続的に使われるものは、最大定格=連続定格である必要があります。言い換えると、常に走り続けられるマラソンランナーのような性格が期待されます。一方、出力密度を高めに設定する場合、余裕を削っていると考えることができます。通勤電車のように、加減速する短時間は大きな出力が必要だが、巡航時には小さな出力でよい場合は出力密度を高めに設定することになります。マラソンランナーと対比させると短距離選手のような性格になります。
今回の検討では、
出力;1(kW)、2.5(N・m)/4000(rpm)
入力;200(V)/7(A)
のモータを計画しているとします。1(kW)のモータに出力密度を当てはめると、重量は1~3.3(kg)の範囲で作ることになります。前述のように1(kg)は高性能なスピードランナーで、3.3(kg)はタフなマラソンランナーになります。
要件が定める出力の大小とその必要な定格時間などについて考慮して出力密度を設定します。ただし、この段階ではあまり悩んでも仕方がありませんのでエイヤで決めてしまいます。ここでは、日本人らしく中庸の2(kg)で計画するとします。
モータ材料の比重を鉄の7.8(g/cc)とすると、2(kg)を実現する体積256(cc)となります。256(cc)になる外径と積厚の組み合わせは複数存在します(表1)。
表1 256ccになる外径と積厚の組み合わせ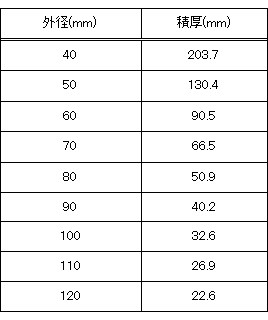
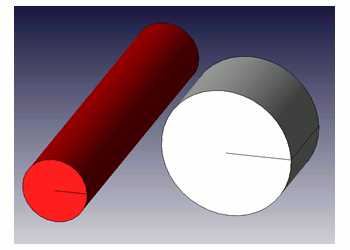 図2 同体積のφ40/L200とφ80/L50の円柱
図2 同体積のφ40/L200とφ80/L50の円柱
同じ体積でも細長いものと太短いものでは雰囲気がかなり異なります。
これでも重量は同じですから、決めるのは難しいといえます。
この組み合わせから要件に沿って選択します。機器への組み込みやすさや設置のしやすさ、製造しやすさなどが判断材料になります。ここでは、比較的中庸なφ80(mm)×L51(mm)とします(図2)。
次にロータ径を決めます。インナーロータであればロータ径はステータ径の50(%)に設定するとバランスが良いです。大径になるほどパーセンテージは上がる傾向にあります。また、アウターロータは70~90(%)にまとまる場合が多いです。ここでは、標準的なインナーロータを採用し、ロータ径はステータ径の50(%)のφ40(mm)と決めます。
次に極数を決めます。極数を決める場合の目安とするのは磁石の大きさやスロット数になります。1極あたりの磁石の大きさが極端に小さい場合や大きい場合、性能が出にくかったり、磁石が作りにくかったりします。目安としては磁石幅が10(mm)~100(mm)になるように設計するのが適当です。ここでは、ロータ径をφ40と決めましたので、ロータの周長は125.7(mm)となります。4極であれば周長は31.4(mm)となり、磁石が小さすぎず大きすぎず適当と思われるので4極にします。
極数を4と決めたので、スロット数は集中巻であれば6、分布巻であれば12か24となります。今回は比較的積厚があるので、分布巻を採用する事とします。集中巻はコイルエンドの高さを低く出来るので、積厚の小さい薄型のモータでメリットが活きてきます。また、1(turn)のコイルが短いので銅損も低くなります。一方、分布巻はコイルエンドが高くなりますが、極あたりのスロット数を増やせるので、弱め界磁制御の効果が出やすく、鉄損や磁石渦電流損も低くしやすいメリットがあります(図3)。
 図3 集中巻(上)と分布巻(下)
図3 集中巻(上)と分布巻(下)
集中巻はスロットピッチが1なので他の相のコイルに重ならないため
コイルエンドの高さを抑える事が出来ます。
分布巻はスロットピッチが3以上になるため、
コイルエンドの高さが高くなり、モータ長が伸びてしまいます。
分布巻でもスロットピッチ(弧長)は24スロットの場合は5.2(mm)、12スロットの場合は10.5(mm)となります。スロットピッチが10(mm)を下回ると製造しにくい面があるので、ここでは12スロットで検討を進めることとします。
極数を決定するのは比較的大きな判断ですがモータ内部の変更に留まるので、外形や出力のように他への影響外小さいので、詳細設計を進めていく段階でも変更する事は出来ます。集中巻と分布巻の変更やスロット数を変更も詳細設計の検討中に変更可能ですので、ここではあまり悩まずに次の検討を進めていくこととします。
トルク密度(推力密度)を確認
前節では要求出力から大方の体格を決めました。その際、出力を短時間発揮すれば良いのか長時間発揮する必要があるかが、判断材料になることを示しました。しかし、世の中には短時間という限定を付けてもやれない事もあります。人間で言えば、50(km/h)で走るとか、400(kg)を持ち上げることはオリンピック選手をもってしても不可能です。モータに当てはめると、重量あたりに取り出せるトルクがそれに当たります。磁気回路には磁気飽和という現象がある事は皆さん御存知と思います。これがトルク(推力)と大きな関係性があり、単位体積あたりに出せる力には上限があり、そのしきい値は磁気飽和により決まることを示しています。
トルクはモータの幾何形状に依る部分もあるため、より一般的な量である推力密度で評価することをお勧めしています。要はギャップ面積あたりの推力に相場値があるという考え方です。モータがトルクを発生している箇所はロータとステータが対向するエアギャップ部です。従って、ここの面積と力がトルクの大小を左右します。ギャップの面積は積厚、ロータ径から決まります(図4)。
 図4 モータのエアギャップ部
図4 モータのエアギャップ部
目標トルクにロータ半径を掛ければ、ギャップ面で発生すべき半径方向推力を求める事が出来ます。推力になって時点で、ロータ径の寄与が消え、単位面積あたりの力のやりとりになります。機械工学的にイメージすると、エアギャップを介してロータとステータにねじり剪断応力が生じている形になります。
ロータ径をφ40(mm)、積厚を51(mm)としましたのでギャップ部面積は6409(mm^2)となります。また目標トルクは2.5(N・m)に設定しているので、ロータ半径20(mm)で割って125(N)の推力を必要とする事がわかります。125(N・m)を6409(mm^2)の面積で担う事になるので、単位面積あたりの推力密度は0.0195(N/mm^2)となります。
推力密度の相場値は0.02~0.06(N・m)と言われています。今回の、0.0195は多少余裕がある事がわかります。ここに余裕があるということはトルクに余裕があると言うことですから、積厚を減らしたり、ロータ径を下げたりできる可能性があることが予想されます。
今回は、トルク密度に注目しましたが、他にも発熱量と放熱量のバランス等を決める熱的なバランスや、材料の使用量からコストの目論見なども、この時点である程度見積もっておく必要があります。
磁路形状を決める
体格により大枠の寸法が決まり、トルク密度(推力密度)の目論見値も決まりましたので、いよいよモータの磁路の形状の寸法を決めていきます。ポイントはモータの中を流れる磁束を必要にして十分な面積を確保するために、ステータのティース幅、ヨーク厚、ロータのヨーク厚を決めて行くことになります。
モータ内の磁束は循環しており、漏れ磁束分も含めて湧き出したり消失したりしません。従って、磁束が循環する流路を維持できる様に各部の寸法を決める事になります。見積もる際はギャップの磁束が基準となります。
ギャップ磁束密度は0.6~1.0(T)程度で使われる場合が多いです。この磁束を循環させるのに邪魔にならない十分なスペースを確保する事が目安になります。ステータのティースはケイ素鋼板なので、飽和磁束密度は1.6~2(T)を期待できます。透磁率が高い分ギャップ磁束分を余計に通すことが出来ますので、その分幅を狭めることも出来ます。
ステータヨーク部はステータティース部から廻ってきた磁束を隣の極に流すのが目的ですので、ティースの本数から大体予想を立てることが出来ます。
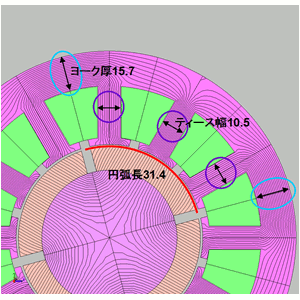 図5 ステータの寸法の決め方
図5 ステータの寸法の決め方
磁極の円弧長は31.4(mm)としました。この磁石から発される磁束を3本のステータティースで引き取る為には31.4(mm)の1/3である10.5(mm)の幅が必要となります。ティースを上がってきた磁束はステータヨークで左右に分かれて隣の極に行くので、ここは31.4(mm)の1/2である15.7(mm)の厚みが必要になることが分ります。
ただし、磁石の残留磁束密度はネオジム焼結でも1(T)程度ですし、ギャップの磁気抵抗などを考慮すると動作点は0.6~0.7(T)程度が見込まれます。一方、ステータティースの材質はケイ素鋼板で1.4(T)は軽く期待できるので、2倍程度の磁束を流せることが期待できます。従って、ティース幅は1/2として5(mm)、ステータヨーク厚は8(mm)に設定することにします(図5)。
ロータヨークも同様の考え方をします(図6)。磁石から流れ込んだ磁束を隣の磁石に流し込むことになるので、円弧長31.4(mm)を1/2にして15.7(mm)必要になる事がわかります。SPMで良く使われる炭素鋼も1.6~2(T)の飽和磁束密度は期待できるので、ステータティース同様1/2の8(mm)にします。
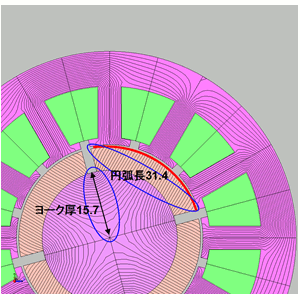 図6 ロータの寸法の決め方
図6 ロータの寸法の決め方
コイル巻数を決める
トルクは磁石磁束と電流の積により生じるので、コイルの巻数を決める作業は磁石の量を決める作業と等価です。多量の強力な磁石を配すれば、電流アンペアターンは小さくて済みます。逆に少量の磁石でも電流アンペアターンを大きくすれば、トルクを得る事が出来ます。電流アンペアターンというのは、電流×巻数のことです。電流100(A)と巻数1(turn)と電流1(A)と巻数100(turn)は電磁石の強さの面では同じになります。トルクと鎖交磁束、電流の関係は、
トルク(N・m)=極大数×鎖交磁束(Wb)×相電流(A)
ですので、最大トルクは2.5(N・m)、極対数は2、最大相電流は7(A)なので、鎖交磁束数は1.79(Wb)必要なことが分ります。ギャップ面積は予め決めているので、磁石の強さ(磁束量)とコイル巻数を調整する事になります。1.79(Wb)になるコイル巻数とギャップ磁束数の組み合わせを表2にまとめます。
表2 1.79(Wb)になるコイル巻数と鎖交磁束の組み合わせ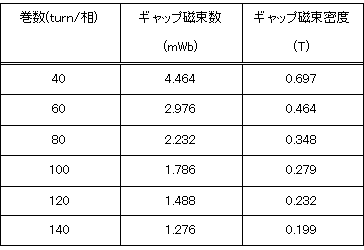
SPMのように希土類磁石を置けるだけ配置した場合、ギャップ磁束密度は0.6(T)程度になります。磁石をV字に配置するなどして磁石磁束を増やすことで更に磁束密度を高めることも出来ます。磁束密度が高いとコギングトルクが大きくなったり鉄損が増えます。エアギャップは電機子磁束も通りますので、磁石で埋めきってしまうと磁気飽和しやすくなる危険性もあります。そもそも希土類磁石は高いのでコストを跳ね上げるリスクを持っています。
逆に磁石を減らすことでギャップ磁束数を減らすことが出来ますが、その分コイル巻数が増えていくことが分ります。同じスロット面積に巻くコイル巻数が増えるということは、1本あたりのコイルを細くするしかありません。また、巻数を増やした分だけコイルが長くなります。例えば巻数を二倍にすると断面積が半分になって長さが二倍ですから、抵抗は4倍に増加し、銅損も4倍に増加することになります。ここでは、比較的磁石を多めに使うとして60(turn)で進める事にます。
コイル断面積と通電可能な電流の間にも目安値があり、10(A/mm^2)と言われています。したがって7(A)を連続通電するためには0.7(mm^2)程度を確保したいので、φ1.0の線が目安となります。巻数を60と決めたので、必要なスロット面積は0.7×60=42(mm^2)となります。しかし、スロット内にコイルを隙間なく挿入することは不可能です。占積率の相場値としては40~60(%)なので、50(%)いけるとして84(mm^2)の面積が必要になります。先ほど決めたステータ形状のスロット内に入る台形は上低5.4(mm)、下底11.7(mm)、高さ11.6(mm)なので面積は99.18(mm^2)となりましたので、とりあえずスロット内に60ターンのコイルが収まりそうなことが確認出来ました(図7)。
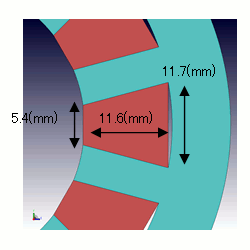 図7 スロット面積
図7 スロット面積
コイルの巻数60(turn)、線径φ1.0(0.7mm^2)の他にステータ形状等々が決まりましたのでコイルの抵抗値を確認することができます。最初にコイル1(turn)の長さを求めます。軸方向の長さはステータの積厚51(mm)にコイル端部の高さ分を片側40(mm)と見込んで91(mm)、周方向の円弧長さは径をギャップ径40 (mm)にスロット深さ分+20(mm)として極数で割ると47.1(mm)になります。従って1(turn)あたりの長さは
((51+40)+47.1)×2=276.2(mm)
になります。ここで巻数は60、極対数は2なので1相あたりの長さは33.1(m)になることが分ります。
276.2×60×2/1000=33.1(m)
意外に長い銅線を巻く必要がある事がわかります。素線断面積は0.7(mm^2)、銅の抵抗率は1.68e-8(ohm m)なので、抵抗値は1相あたり0.79(ohm)になることが分ります。
33.1×(1.68e-8)/(7e-7)=0.79(ohm)
電流は最大7(A)通電しますので、相あたり39(W)の銅損が発生する事がわかります。
銅機械と鉄機械
この磁石磁束とコイル巻数のバランスを検討することを”装荷を決める”と言う言葉を使う場合があります。磁気装荷はギャップ磁束密度のことを指し、電気装荷はコイルの巻数と電流の積を示し、比電気装荷はギャップ部の単位長さあたりの電気装荷のことを示します。モータの出力は電気装荷と磁気装荷の積で決まりますので、この装荷を決める事がモータ設計の根本となります。コイル巻数を多めにして電気装荷を増やしてモータ内の起磁力源を銅線に期待するもの銅機械、磁石や鉄心に期待するものを鉄機械と呼び、モータの性格付けをします。
初期設計案の確定
ここまでで、初期設計案をまとめることが出来ました。得られた諸元を表3に示します。
この初期設計案が要件を満たしているかが最初のハードルとなります。出力は足りているか、体積や重量が要件を満足しているかなどを確認します。ただし、あくまで初期設計案ですから、多少の過不足は厳密に考える必要はありません。この設計案を叩き台として、細かい部分の検討をスタートさせて、完成度をどんどん高めていくことになります。叩き台を叩いて叩いて良いものを作るのが設計者の仕事ですから頑張って下さい。
検討結果が要件とあまりにもかけ離れている場合は注意が必要です。大体の場合は初期設計過程の何処かでミスを犯しているので、検討過程を再確認して下さい。何度検討しても、要件との差異を埋められない場合に限って、要件自体が無理を強いていないかを要件を決めた企画者に確認することになります。ただし、企画者の確信犯の場合も多いので変更はあまり期待できない可能性が高いでしょう。その場合は覚悟を決めて全力で課題に当たってください。きっとその結果がベストの解になりますから…。
表3 初期検討で決定した諸元
| 項目 | 仕様 |
|---|---|
| 形式 | インナーロータSPM |
| 極数 | 4 |
| スロット数 | 12 |
| ステータ外径 | φ80(mm) |
| ロータ外径 | φ40(mm) |
| 積厚 | 51(mm) |
| コイル巻数 | 60(turn/極) |
| コイル抵抗 | 0.77(ohm/相) |
| コイル線径 | φ1.0(mm) |
| 最大電流 | 7(Apeak) |
| コア | 50A400 |
| 磁石 | ネオジ焼結 |
| 重量 | 2(kg) |
| 最大トルク | 2.5(N・m) |
| 最高回転数 | 4000(rpm) |
| 出力 | 1(kW) |
次回は詳細を検討
先号でも御紹介しましたとおり、ここまで行った検討は設計ツールJMAG-Expressを活用することで簡単に行う事が出来ます。形状の変更などを容易に行うことができますし、解析結果を瞬時に得られますので、各部寸法のバランスを考慮しながら試行錯誤を行う初期検討のフェーズには適したツールですので、是非お使い下さい。
次号では、今回得られた初期設計案をJMAG-Express Public上で評価してみます。設計パラメータと並行して、での情報公開やセミナー実施なども計画しておりますので、こちらもご期待いただければと考えております。
(坂下 善行)
コラム 銅機械と鉄機械
モータ設計講座ではモータ設計の流れを中心に解説しておりますが、そこでは説明しきれなかった話題をこのコラムで取りあげ、JMAGを使って簡単な検証結果と突き合わせることで、より深く解説したいと考えています。
今回の話題は電気装荷と磁気装荷、銅機械と鉄機械について取り上げてみたいと思います。モータ設計の現場では電気装荷、磁気装荷という言葉が使われていますが、私はいまいちピンときませんでした。ただ、モータの動作原理を煎じ詰めると磁石磁束のコイル磁束の積に行き着くので、おそらく磁石磁束とコイル磁束に関係あるだろうなあと、おぼろげながらイメージしていました。教科書を紐解くと磁気装荷とは「ギャップ磁束密度」のことを示し、比電気装荷とは「電機子ギャップの周方向単位長さあたりのアンペアターン」のことを示すとあり、当初思っていたイメージが概ね合っていることが確認できました。(参考資料:電気機器設計第二次改訂版;電気学会)
モータを設計するにあたり、磁気装荷と電気装荷の両方を高める事ができれば、性能が向上するわけですが、御存知のとおり磁気飽和の影響であるため磁気装荷(=ギャップ磁束密度)には限界があるので無闇に上げられません。電気装荷に関してもアンペアターンが増えていくと熱的に極めて厳しくなりますし、体積や重量が増加しますので、こちらも無闇には上げられません。従って、装荷をバランス良く決めると言うことは真にモータ設計をしていることになるわけです。まあ、今まで装荷という言葉を意識していなかっただけで、普段やっているモータの設計検討に他なりません。設計において“装荷を気にする”とは、なにか新しい指針を示すものではなく、従来どおりギャップや磁気回路の磁束密度、コイルの電流密度などを良いバランスで設計しなさいと言っていることになります。
似たような言葉として、銅機械と鉄機械という言葉もあります。比電気装荷の大きな機械を銅機械といい、ギャップ磁束密度が高く磁気装荷の大きい機械を鉄機械といいます。PMモータの場合、銅機械はコイル磁束主体の機械になります。磁石を減らすことで磁石のコストを抑えることができますし、無負荷時や低負荷時のギャップ磁束密度が低くなるので鉄損は減ります。一方、コイルの巻数は相対的に多くなるので、スロット面積が同じであれば、コイル巻数が増えた分だけコイルを細くする必要があり、銅損が増加します。一方、鉄機械は磁石磁束主体の機械になります。同じトルクを出すためのコイル巻数を減らせるので、大トルク時の銅損を減らせます。ただし、磁石を沢山使うのでコストは上がります(モータ材料の中では磁石の重量単価は大分違います)。また、無負荷でもモータ内部が高磁束密度になるので、軽負荷でも鉄損は総じて高めになってしまう欠点があります。
言葉では分かり難いと思いますので、実際にJMAG-Express Publicを使って簡単な実験を行い、その結果を示します。外径φ80(mm)、積厚50(mm)のSPMモータです。基準のロータ径をφ40(mm)とし、銅機械としてロータ径をφ30(mm)に下げたもの、鉄機械としてφ50(mm)に上げたものの結果を比較します。尚、ロータ径を変える事で磁石の量が変わりますので、7(A)時のトルクが変わらないようにコイル巻数を調整します。この結果、トルク定数は一定に保たれますが、磁石の作る総磁束、コイルのインダクタンス、銅損、鉄損のバランスが変化します。
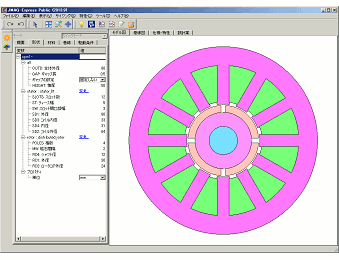
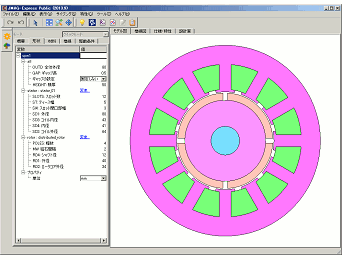
 図1 モータ形状 銅機械_φ30(上)と鉄機械_φ50(下)と初期設計案_φ40(中)
図1 モータ形状 銅機械_φ30(上)と鉄機械_φ50(下)と初期設計案_φ40(中)
実験の結果を表1に示します。予想したとおり銅機械は鉄損が押さえられましたが、銅損は逆に増えてしまいました。これは総磁束数が減った分を巻数で回復したため、巻数を増やしている素線径が細くなり相抵抗が40%弱増加しているためです。巻数を増やしているためインダクタンスも増えています。トルク定数を一定に揃えているので誘起電圧は同じになりますが、インダクタンスが増えている分だけ高回転で回りにくくなることが予想されます。
鉄機械は予想どおり鉄損が増加していますが、意に反して銅損も増加しています。これはロータ径を大きくしたのに伴い、スロット面積が狭くなってしまい、巻数を減らしているにも関わらず、コイルを若干細くする必要が出てしまったためです。
表1 設計パラメータとモータ定数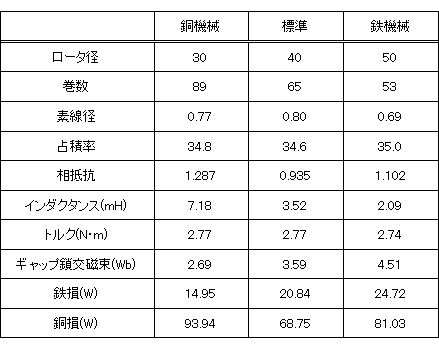
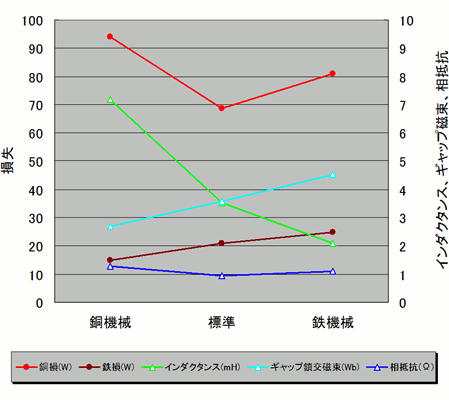 図2 モータパラメータの感度
図2 モータパラメータの感度
[JMAG Newsletter 2014年1月号より]