ソルバー [機能]

磁石渦電流高速計算

モータの磁石に発生する渦電流の評価は、3次元モデルを用いた解析を必要とするため計算時間を要していました。本機能を用いることで、より高速に解析を行えます。
例えば、従来の手法では8時間かかっていた磁石の渦電流損失計算が、約12分で結果を得られます。

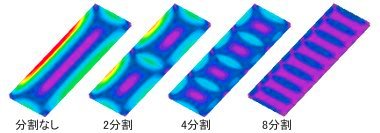磁石分割数ごとの渦電流損失

動画による機能紹介

磁石渦電流解析

透磁率分布を考慮した解析

本機能を用いると、材料の磁化特性を特定の状態に固定して解析するため、磁束密度分布や磁束線を要因毎に分離して評価することができます。
トルク分離事例

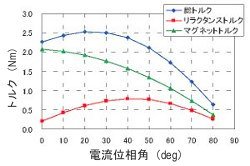トルクの電流位相角特性の分離

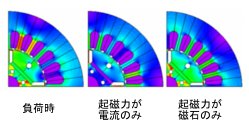磁束密度分布の分離

動画による機能紹介

モータのトルク分離解析

減磁計算

反磁界減磁や熱減磁がモータ特性等に与える影響を解析します。反磁界が引き起こす局所的な減磁や、保磁力分布磁石における端部での減磁耐性の違いなどを詳細に評価します。
減磁前の磁石における磁束密度を基準とし、磁束密度分布の変化を減磁率として追うことができます。パーミアンス係数分布と合わせて分析することにより、磁石を詳細に分析します。

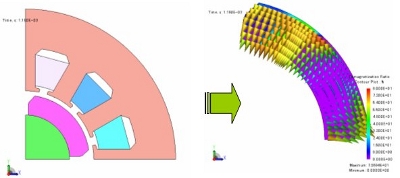PMモータの減磁率分布

動画による機能紹介

モータ磁石の減磁解析

時間周期補正法

時間周期補正法は磁界解析における変動場の時間的な周期性を利用します。過渡解析の初期に生じる過渡状態を抑えて、少ないステップ数で定常解を算出します。この機能は、外部回路に電位（電圧）源を用いた磁界解析モデル、特に時定数が長く、定常解に至るまでに多くの解析時間（解析ステップ）を必要とするモデルに有効な高速解法です。JMAG独自の技術が盛り込まれており、ほとんどの時間周期的な変動場を持つ問題に対して、制限なく適用することができます。過渡的な初期状態が長く続く誘導機とスイッチングトランスの解析を取り上げ、従来の解法と比較した事例を示します。
誘導機の解析はインダクタンスに由来する時定数の大きさから、定常状態に移行するまでに10周期以上もの電気角が必要な場合も珍しくありません。この過渡状態をいかに短く抑えるかが、解析上のポイントでした。今回、時間周期補正法を採用したことにより、定常状態に移行するまでの解析時間を大幅に減らすことができました（図1）。また誘導機の解析では従来の擬似定常との併用により、この手法の単独利用に比べて更なる解析の高速化が可能です。

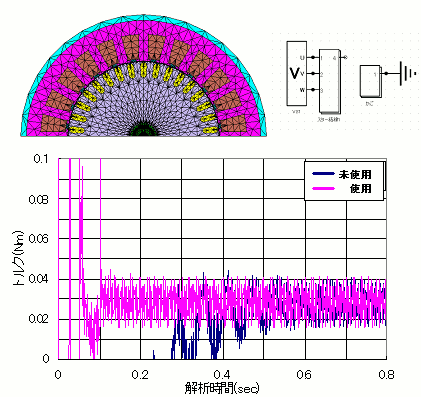図1　誘導機解析における
時間周期補正法使用時/未使用時の定常トルクへの収束の比較

次にスイッチングトランスの解析では、2次側の平滑コンデンサの容量が時定数を決めており、その容量によって、時定数が解析の時刻刻みに比べて非常に大きくなるケースがありました。このため従来の手法では、定常状態に移行するまでの解析時間を多く要する問題でしたが、本手法を用いることで、解析時間の大幅な短縮を可能にしています（図2）。

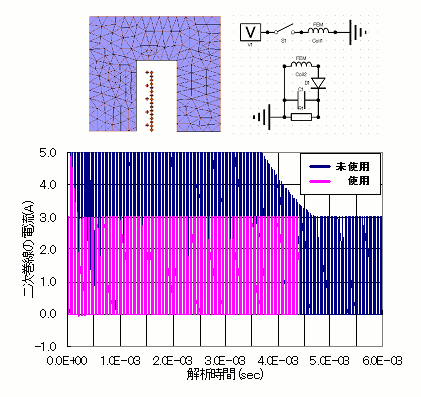図2　スイッチングトランス解析における
時間周期補正法使用時/未使用時の定常電流への収束の比較