目次
1. 概要
2. 周波数に依存しない異常渦電流損失モデリング
　2.1 モデリング
　2.2 異常渦電流損失係数\(C (B )\)と指数\(\alpha\)の同定
　2.3 同定結果
3. 提案モデルの適用
　3.1 他周波数への適用
　3.2 異なる材料特性を持つリングコアにAC＋7次高調波を与えた場合
4. まとめ
5. 参考文献

1. 概要

シミュレーションによる正確な損失予測は、特に電気自動車で用いられるような高効率の先進的なモータにおいて極めて重要である。モータの主要な損失成分の一つである電磁鋼板で発生する鉄損は、ヒステリシス損失、古典渦電流損失、および異常渦電流損失から構成される。ヒステリシス損失については、プレイモデルを用いることで、近年シミュレーションによる推定精度の向上が図られている。同様に、1次元有限要素法を用いることで、古典渦電流損失の予測精度も向上している。しかし、異常渦電流損失の包括的なモデリングは依然として困難であり、さらなる検討が必要である。モータ内部では、マイナーループのような複数の周波数を持つ複雑な磁束波形が発生するため、このような波形に適したモデル化が望まれている。
本書では、Bertottiモデルをベースとして、新しいモデリング手法を提案する。このアプローチでは、異常渦電流損失が磁束密度の時間微分のべき乗と異常渦電流損失係数により表現されるとしている。まず、事前に測定されたリング試験片の鉄損を正確に再現する指数と異常渦電流損失係数の組み合わせを同定する。次に、得られた指数と係数を材料固有のパラメータとみなし、シミュレーションに用いる。本資料ではそのモデリングの検証として、提案したモデリング技術を交流＋高調波磁束密度を持つ別の材料に適用した。

2. 周波数に依存しない異常渦電流損失モデリング

2.1 モデリング

提案するモデルは、次に示されるようなBertottiモデルと同類の形式をもつ。

(1)

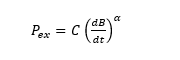
ここで、\(P_{ex}\)は異常渦電流損失密度、\(B\)は磁束密度、\(t\)は時間、\(C\)は異常渦電流損失係数、\(\alpha\)は指数である。
この章では、電磁有限要素過渡応答解析（FEA）での使用を目的とした、任意の磁束密度波形に対する異常渦電流損失モデリングについて説明する。損失係数\(C\)は\(B\)のみの関数であると仮定する。

(2)

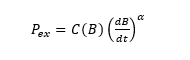
この式において、\(C (B )\)は磁束密度依存の異常渦電流損失係数を表す。\(C (B )\)の具体的な形と値\(\alpha\)の組み合わせは、次節で明らかにする。

2.2 異常渦電流損失係数\(C (B )\)と指数\(α\)の同定

図1に示す測定システムを用いて、交流励磁の周波数を変化させながら、直流バイアス下の交流マイナーループ損失を測定する。測定周波数は1kHz、5kHz、および10kHzである。リング試料には、外径127mm、内径102mmの電磁鋼板35A210を使用し、その直流BH特性は図2に示される。測定された異常渦電流損失\(P_{ ex }\)_{_}\(_ { mes }\)は式(3)で表されるように、測定された全鉄損\(P_{ tot }\)_{_}\(_ { mes }\)と、ヒステリシス損失\(P_{ hy }\)および古典的渦電流損失\(P_{ cl }\)の和との差分として定義される。

(3)

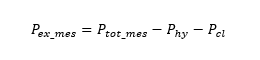
ヒステリシス損失と古典渦電流損失は、それぞれプレイモデルと1次元FEAを用いたシミュレーションにより算出する。これらのシミュレーションによるアプローチでは、表皮効果とマイナーループ挙動の両方が考慮される。\(C (B )\)として、一定値（以下\(C_{ 0 }\)と呼ぶ）と、図2に示すような磁性体の磁化率に基づく形状の関数（以下\(C_\chi(B )\)と呼ぶ）の2種類を比較した。指数\(\alpha\)は1.5、1.8、および2.0の3種類とし、加振周波数に対して、測定された鉄損に最も適合する\(C (B )\)を特定する。最終的には、任意の磁束密度波形に一般的に適用できるように、\(C (B )\)と\(\alpha\)の単一の組み合わせを、周波数依存性を最小限に抑えるように選択する。

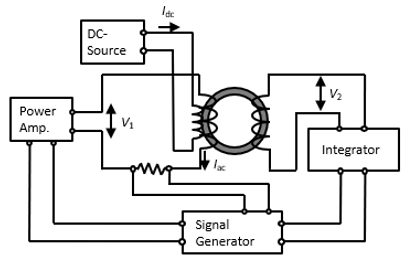
図1　測定システム