目次
1. 概要
2. 超電導体を含む熱・磁界連成解析
3. 無絶縁パンケーキコイルの過電流解析
3.1 解析モデル
3.2 解析結果
4. まとめ
5. 参考文献
1. 概要
超電導機器の運用における主要な課題の一つとして、クエンチの発生が挙げられる。シミュレーションによるクエンチ挙動の正確な予測は、超電導システムを安全性確保と信頼性向上において重要である。
クエンチ現象は、コイルの局所的な超電導状態の崩壊による常電導転移から始まり、この常電導領域におけるジュール熱の急激な発生と伝播が特徴である。超電導状態の崩壊は、温度上昇、電流密度集中、または磁束密度集中により、超電導の臨界条件を超えた際に発生する。クエンチ現象を精密に解析するためには、以下の要素が必要である。
- 超電導体特有の遮蔽電流を適切に表現できる精緻な電磁界モデル
- 温度・電流密度・磁束密度に依存する非線形な超電導材料モデリング
- ジュール熱の発生と熱拡散、および電磁界と熱の相互作用を考慮した連成解析
本稿では、図1に示す、高温超電導体であるREBCO(希土類系銅酸化物)テープ線材を使用した無絶縁パンケーキコイルの解析例を通して、シミュレーションによりクエンチ時の詳細な物理現象を捉えることができることを紹介する。
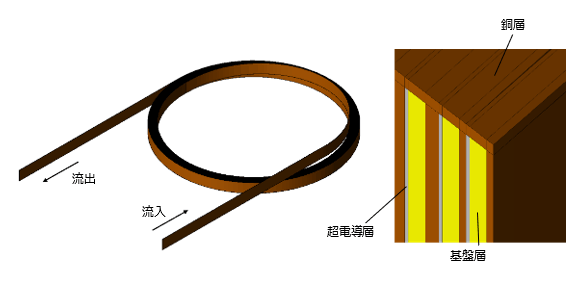 図1 無絶縁パンケーキコイルモデル:モデル全体(左)とコイル断面の拡大図(右)
図1 無絶縁パンケーキコイルモデル:モデル全体(左)とコイル断面の拡大図(右)
2. 超電導体を含む熱・磁界連成解析
Maxwell方程式に基づく磁気ベクトルポテンシャル法(A法)による支配方程式は次式で与えられる。
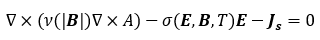
\(B\)は磁束密度、\(A\)は磁気ベクトルポテンシャル、\(E\)は電界、\(T\)は温度、\(\nu\)は磁気抵抗率、\(\sigma\)は電気伝導率、\(J_s\)は強制電流密度をあらわす。電界は電気スカラーポテンシャル\(\phi\)を用いて次式で与えられる。
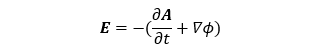
超電導体の電気伝導率について、材料モデルとしてn値モデルを採用する場合、電界、磁束密度、温度に依存し、式(3)のように表される。
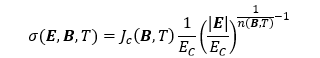
超電導体の電気伝導率が温度に依存するため、熱伝導方程式によって式(4)を解いて温度を求める。
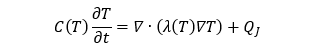
\(C(T)\)、\(\lambda(T)\)、\(Q_J\)は熱容量、熱伝導率、発熱を表す。式(1)から超電導体および常電導体におけるジュール損失を求め、これを式(4)の熱源項として入力し、温度を算出する。得られた温度を次時刻ステップの式(1)の電気伝導率に反映させ、式(1)を再度解く。このように、逐次的な弱連成手法を用いて解析を実施する。
3. 無絶縁パンケーキコイルの過電流解析
3.1 解析モデル
解析に用いたパンケーキコイルモデルの仕様を表1に示す。過電流試験として、0Aから100Aまで0.5A/secの速度で通電した。
表1 コイルの仕様
| 内径 | 60 (mm) |
|---|---|
| 外径 | 66 (mm) |
| ターン数 | 30 |
| テープ幅 | 4 (mm) |
| 銅層厚さ | 20 (μm) |
| 基盤層厚さ | 50 (μm) |
| 超電導層厚さ | 10 (μm) |
『JMAGソフトウェア正規ユーザー(有償会員)』または『JMAG WEB MEMBER(無料会員)』でサインインが必要です。
『JMAG WEB MEMBER(無料会員)』へ登録することで、技術資料やそのほかの会員限定コンテンツを無料で閲覧できます。
登録されていない方は「新規会員登録」ボタンをクリックしてください。



