目次
1. 背景
2. 検証方法
3. 結果
4. まとめ
5. 参考文献
1. 背景
メッシュ分割は有限要素法において精度とICCGなどの反復計算の収束性にかかわる重要な要素である。必要な領域に必要な分解能がないと収束性の悪化もしくは精度不十分といった結果を招くことになる。一般的に要素形状のアスペクト比が高くなると収束性が悪化することもわかっている。
本報告では上記をふまえてコイル周辺の空気領域の要素形状がICCGの収束性、計算精度に与える影響について検証結果を報告する。本検証の背景はコイルの交流損失計算にある。回転機では角線が広く使われるようになり素線の渦電流を計算することが増えている。そうした解析では漏れ磁束を正確に捉えるためにコイルエンド周辺の空気メッシュの分解能を高めることが言われている。ここではどの程度分解能が落ちると精度や収束性に影響するかを調査した。
2. 検証方法
検証モデルとして2本の素線を用意し、片方には強制的に交流電流を通電し、もう片方はその磁場による渦電流が生じるにした(図1)。FEAモデルとして3つのパターンを用意し、それぞれ空気のメッシュを変えて計算を行った。素線内部のメッシュは同一のものを使用した(図2)。モデルAは空気領域の要素サイズを1000mmと大きい値を設定した。モデルBは100mmに設定した。モデルCはモデルBの素線周辺にさらに小さい要素サイズ5mmを設定した。モデルAやBでは素線周辺に蜘蛛の巣状のメッシュが生成されていることが確認できる。素線の要素サイズに対して空気の要素サイズが大きい場合こうした蜘蛛の巣状のメッシュが生成されやすくなる。

(a) 素線形状

(b) 素線のメッシュ
図1 検証モデル
2つの素線の片方に1A, 1kHzの交流強制電流を流す。
もう片方は無通電の状態で渦電流損失を計算する。素線径は20mm、素線間は40mm。
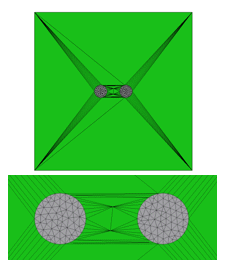
モデルA
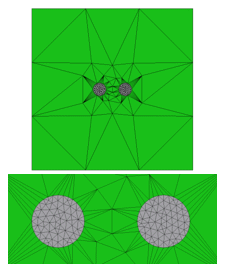
モデルB
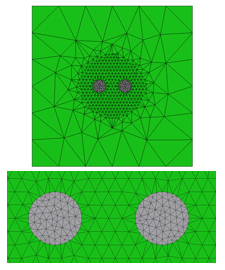
モデルC
図2 素線モデルと空気領域のメッシュ
モデルAは空気領域の要素サイズを1000mm、Bは100mm、CはBの要素サイズにコイル周辺のみ5mmで設定。モデルA、Bではコイルに隣接する空気メッシュの多くが頂点を共有する蜘蛛の巣状のメッシュが確認できる。モデルCでは蜘蛛の巣メッシュが解消されている。
(続く)
『JMAGソフトウェア正規ユーザー(有償会員)』または『JMAG WEB MEMBER(無料会員)』でサインインが必要です。
『JMAG WEB MEMBER(無料会員)』へ登録することで、技術資料やそのほかの会員限定コンテンツを無料で閲覧できます。
登録されていない方は「新規会員登録」ボタンをクリックしてください。



