目次
1. 背景
2. 端部での還流
3. 空間高調波による還流
4. まとめ
5. 参考文献
1. 背景
電磁界解析では、鉄損評価を含めて解析の詳細度と利便性のバランスからFEMによる二次元解析が広く利用されている。モータの効率向上に伴い、鉄損解析にも高い精度が要求されるようになり、解析手法もこれに合わせて進歩してきたといえる。
積層鉄心の渦電流損失解析には、これまでエプスタイン試験により得られた鉄損特性に基づくFFTを利用した解析手法が適用されてきた(以下、従来法)。この手法は、正弦波交流下や低周波域では、一定の成果を収めているが、鉄損特性の存在しない高周波域や直流重畳状態の損失解析では精度が得られない場合がある。これを改善する手法として、鋼板1枚ごとに厚み方向に自由度をもつ磁束密度や渦電流の分布を解く方法(以下1D法)が提案されている。
上記のように二次元解析において鋼板中の渦電流損失を評価する手法が提案されているが、いくつかの課題が残されている。そのうちの一つが鋼板内での還流の表現である。1D法は、面内方向のみの渦電流を考慮する手法のため、還流部分の影響を無視している。一方従来法も通常30mm幅エプスタイン試験による鉄損特性を用いているのでそれとは磁気回路の幅が異なるモデルに適用すると同様の問題を抱えることになる。正確な鋼板内の渦電流損失評価を行うには三次元解析が必要だが、そのためには二次元解析の有効性と限界を知り、精度と計算コスト両面から必要性を判断することとなる。
ここでは、三次元解析と1D法の結果をもとに還流による影響度を評価する。
2. 端部での還流
上記で述べたように二次元解析では鋼板端部での渦電流の還流部分を考慮しておらず、渦電流損失を過大評価する。ここでは板厚dと幅Lの比L/dによって還流を無視することによる影響がどの程度あるのか評価する。図3に示すように板厚0.5mmの鋼板で幅Lを変え、二次元解析の後処理で1D法で渦電流損失を評価した場合と三次元解析で評価した場合を比較した。結果を表1に示す。幅Lが狭くなるほど二次元解析の結果を用いた1D法では渦電流損失を過大評価している。端部の還流を無視している影響は還流部分での渦電流の流路の長さが全体の流路に占める比で見積もることができ、簡易的には(L+d)/Lで算出できる。その値を表1中に示しているが、概ね二次元解析(1D法)の過大評価率に一致している。L=0.5mmではかい離があるが、端部で直角に渦電流が還流しないことや表皮効果が関連していると考えられる。(続く)

ロータ表面の渦電流分布(三次元解析)
ギャップ側からロータ表面を見るといくつもの渦が確認できる
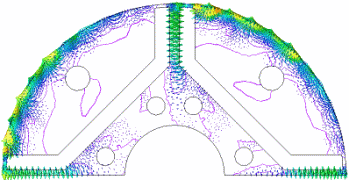
スロット高調波分布
線は磁束線、ベクトルは渦電流を表している
『JMAGソフトウェア正規ユーザー(有償会員)』または『JMAG WEB MEMBER(無料会員)』でサインインが必要です。
『JMAG WEB MEMBER(無料会員)』へ登録することで、技術資料やそのほかの会員限定コンテンツを無料で閲覧できます。
登録されていない方は「新規会員登録」ボタンをクリックしてください。



