目次
1. 背景
2. 時間周期有限要素(TP-FEM)法と時間周期補正(TP-EEC)法
3. 知っておくべき大切な仮定
4. まとめ
5. 参考文献
1. 背景
電気機器設計においては、限られた設計期間内で最良の製品を作るためにComputer Aided Engineering(CAE)ソフトウェア、特に、電磁界有限要素解析(FEA)が形状再現性の高さや材料の非線形性の取り扱いやすさを理由としてよく用いられる。JMAGもそのひとつであり、処理時間短縮はソフトウェア利用者の強い要望である。これを達成するため、JMAGにおいては非線形反復解法の改良、ICCG求解法の改良、またメニーコアを有効利用することを目的とした共有メモリおよび分散メモリ型並列処理の改善などが行われている。
渦電流解析など時定数が大きい問題において、定常解を得るために多くの時刻ステップを必要とする。この対策として、時間周期有限要素法(TP-FEM法)が提案されている。この手法では過渡状態を経ず、定常解を直接求解することが可能である。一方で、解くべき連立一次方程式の次元は一時刻ステップあたりの未知数と、一周期ないしは半周期の時刻ステップ数の積となり、計算コストに難点がある。この課題を克服するため、近年では時間周期補正法(TP-EEC法)が提案されている。この手法では、TP-FEM法をベースとし、そこにExplicit Error Correction法(EEC法)を適用することで、時間的に収束が遅い誤差成分を取り除く。
一般的なTP-EEC法の効果や性能に関しては先行研究が多く存在するため、そちらを参照してほしい。
本稿では、JMAGで採用しているTP-EEC法についてその具体的処理とTP-EEC法の適用の可否について説明する。読者ご自身のモデルへの、適用可否判断の材料としていただきたい。
2. 時間周期有限要素(TP-FEM)法と時間周期補正(TP-EEC)法
前述のとおり、TP-EEC法のベースはTP-FEM法である。そこで、本節ではまずTP-FEM法について説明する。式(1)を反復法などのソルバで求解し、一周期分の結果を一度に得る方法をTP-FEM法と呼ぶ。(続く)
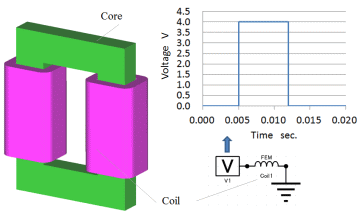
リアクトルモデル
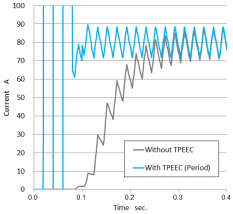
周期性のTP-EEC法を適用した場合の電流履歴
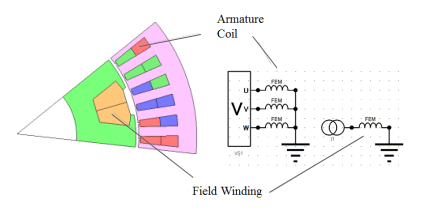
同期回転機モデル
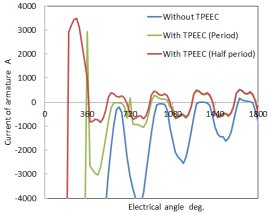
電機子コイル巻線電流履歴
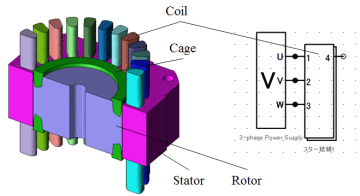
誘導機モデル
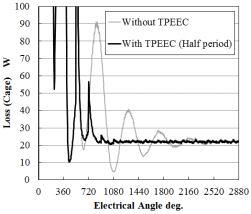
かごの損失履歴(すべり0.1)
『JMAGソフトウェア正規ユーザー(有償会員)』または『JMAG WEB MEMBER(無料会員)』でサインインが必要です。
『JMAG WEB MEMBER(無料会員)』へ登録することで、技術資料やそのほかの会員限定コンテンツを無料で閲覧できます。
登録されていない方は「新規会員登録」ボタンをクリックしてください。



