目次
1. 概要
2. 従来のFEAを用いた電磁機器の振動計算手法
3. 提案する伝達関数を用いた電磁機器の振動計算手法
4. 対象モデル
5. 伝達関数の作成
6. 精度検証
　6.1　比較条件
　6.2　検証結果
7. 適用事例
8. 適用限界と実用上の課題
9. まとめ
10. 参考文献

1. 概要

EVパワートレインに代表されるモータ搭載機器において、高効率・高出力化は常に要求されているが、近年では低騒音・低振動化の要件も高まっている。その騒音・振動の加振源の要因として組込モータの電磁力があり、その影響が大きいことが知られている。一方で、実設計では磁気設計とNV（騒音・振動）設計が独立に進められる傾向にあり、設計の手戻りを引き起こす一因となっている。磁気特性とNV特性を同時に考慮した設計を行うことでこれらの課題は解決されるが、システム全体を含めた振動解析は計算コストが高く、新たに設計フローに含めるハードルが高い側面もある。振動計算コストの短縮手段として、電磁力を入力、振動を出力とした伝達関数を援用してシステムの振動特性を表現する手法が採用されている。
本稿では、モータ磁気特性とシステムNV特性を同時に考慮した設計を実現するための、伝達関数を援用したシステムレベルNV設計フローを提案する。

2. 従来のFEAを用いた電磁機器の振動計算手法

電磁機器の振動・騒音の発生メカニズムは、起振源である電磁振動と、構造体が共振・増幅する事により発生する。CAEでこのメカニズムを再現するためには磁界－構造の連成解析が必要である。まず電磁界解析により電磁力分布を求め、得られた電磁力を入力として振動・騒音解析を行う。ここでは、変形による電磁界への影響はないと仮定して、磁界－構造の一方向連成解析を行うことを想定する。従来のFEAを用いた電磁機器の振動計算フローの概念図を図1に示した。FEAによる系全体の構造解析は3次元モデルかつ広範の領域の計算となるため要素数が多くなり計算コストが大きくなる傾向にある。

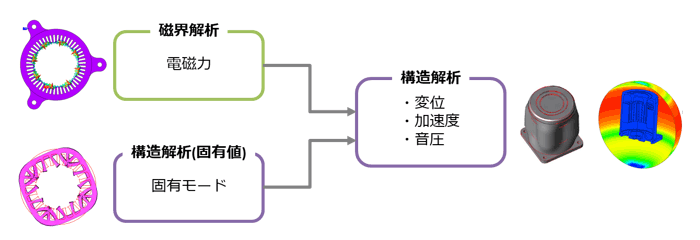
図1　従来のFEAを用いた電磁機器の振動計算フロー

3. 提案する伝達関数を用いた電磁機器の振動計算手法

FRF:周波数応答関数と呼ばれる、ある点に作用した単位荷重に対する別の自由度の応答を表現する伝達関数を用いて加振力を入力とした振動応答を出力させる。次式で表される。

\([X]=[G][f]\)　　　　(1)

ここで\(X\)は振動応答、\(G\)は伝達関数、\(f\)は加振力である。ここではシステムの加振源がモータから生じる電磁加振力のみとして扱う。伝達関数を用いた電磁機器の振動計算フローの概念図を図2に示した。伝達関数を介して電磁力から振動応答へ直接変換するため瞬時に振動応答結果を得ることが可能な利点がある。

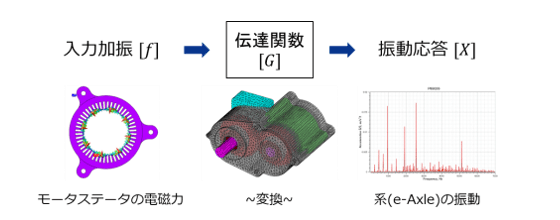
図2　伝達関数を用いた電磁機器の振動計算フロー