目次
- 回転機の銅損解析
- ズーミング法の手順と概要
- ズーミング法の回転機銅損への適用
3.1 2次元のIPM回転機の銅損特性解析
3.2 回転機におけるリッツ線の損失解析 - まとめ
- 参考文献
1. 回転機の銅損解析
回転機巻線の渦電流を考慮した銅損の有効な解析方法として有限要素法による電磁場解析が挙げられる。この方法では計算精度が得られる反面、素線を一本ずつモデル化する必要があるため、メッシュ生成した際の要素数が増加して計算時間が膨大になるという欠点がある。
このような問題の汎用的な計算コスト低減の手法としてズーミング法(1)がある。この手法は、はじめに粗いメッシュで全体の場を解き(全体解析)、その結果を引継ぎ、精度を得たい部分のみを詳細にモデル化して解析を行う(部分解析)手法である。これにより全体・部分の各解析の要素数を削減して収束性を向上することが可能となり、計算時間の短縮が図れる特徴がある。
先行例として文献(2)では磁束密度分布を、文献(3)や文献(4)では境界上のベクトルポテンシャルを全体解析から部分解析へ引き継ぐ方法がそれぞれ提案され、良い結果が得られている。
一方、回転機を対象としたズーミング法による解析の計算時間や精度の評価は十分ではない。そのため本稿では、本手法を2次元回転機の素線の銅損特性解析および3次元回転機のリッツ線の損失解析に適用し、計算精度と計算速度の改善について評価を行った。以降では、特に断りがない限り、境界上のベクトルポテンシャルを引き継ぐ方法をズーミング法と呼ぶ。
2. ズーミング法の手順と概要
まず全体解析を行い計算する時刻歴すべてのベクトルポテンシャル値を得る。次に部分解析では、精度を得たい部分の細かいメッシュを作成すると同時に、全体解析で計算した場の情報を引き継いだ計算を行う。その引き継ぎには各時刻歴のモデル境界上にあるベクトルポテンシャルの接線方向成分を用いる。全体解析と部分解析で内部の強制電流、透磁率、電気伝導率の分布が同一であれば、内部の磁束密度Bや渦電流密度Jeの分布が同一になることが保証される(5)。
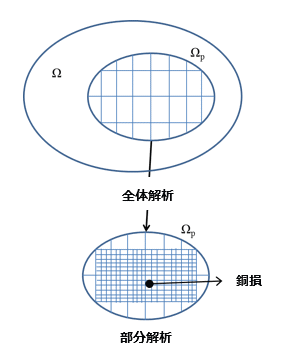
図1 ズーミング法の概念
3. ズーミング法の回転機銅損への適用
3.1 2次元のIPM回転機の銅損特性解析
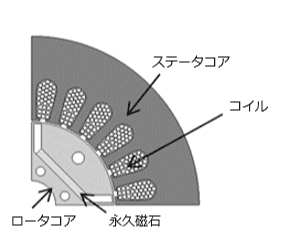
本節ではズーミング法を2DのIPM回転機の銅損特性解析に用いた事例を示す。解析対象は電気学会Dモデル(6)とし、各回転数における銅損特性の計算にズーミング法を適用し、計算精度と計算速度を明らかにする。
表1に検討の際のモータの詳細条件を示す。解析の時間刻み幅は電気角1周期を192分割した。入力は電流とし、波形は回転数によらず同じ振幅で周波数のみ異なるものとした。また解析領域はモデルの対称性から1/4モデルとしている。これらの条件はズーミング法を用いたかどうかにかかわらず共通となっている。
表1 モデル詳細
| 極数 | 4 |
|---|---|
| スロット数 | 24 |
| 線径(mm) | 0.65 |
| 巻数/相 | 140 |
| 電流の振幅(Arms) | 3 |
| 相数 | 3 |
| 回転速度(rpm) | 500, 1500, 3000, 5000, 7000, 10000 |
図2にズーミング法を用いない場合の解析モデルを示す。図2(a)に示すように素線1本ごとにモデル化し、図2(b)のように素線中のメッシュを細分化した。
(a) 解析モデル
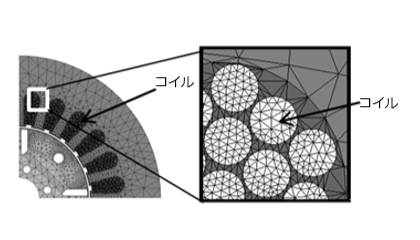
(b) 有限要素メッシュ(空気領域なし)
図2 ズーミング法を用いない場合の解析モデル
『JMAGソフトウェア正規ユーザー(有償会員)』または『JMAG WEB MEMBER(無料会員)』でサインインが必要です。
『JMAG WEB MEMBER(無料会員)』へ登録することで、技術資料やそのほかの会員限定コンテンツを無料で閲覧できます。
登録されていない方は「新規会員登録」ボタンをクリックしてください。



