目次
概要
1. 制御・回路連成時の定常状態を評価する時の課題
2. 提案手法の課題
3. JMAG-RTモデルの分解能の設定
3.1 モータ
3.2 分解能と磁束量の誤差
3.3 計算時間および結果の比較
4. まとめ
5. 参考文献
概要
モータ磁気回路設計では、インバータのスイッチングによる高調波鉄損などを把握するために、FEAと制御回路の連成解析を行う[1]。FEAと制御回路の連成解析は過渡状態が発生し、計算時間がかかる場合がある。
本稿では、モータの高精度な等価回路モデルを用いて過渡状態の早期定常化を図り、定常状態到達後にFEAモデルで計算する方法で計算高速化を試みた。その結果、FEAモデルと同様の精度を持つ等価回路モデルを用いると、全時刻をFEAモデルで計算する場合と比較して、1/2に計算時間を短縮できる事が分かった。
1. 制御・回路連成時の定常状態を評価する時の課題
モータの性能評価の多くは定常状態で行う。制御・回路連成をおこなった際に過渡現象が生じると、定常状態まで電気角数周期分計算する必要がある。特にPWMキャリアの電流波形を捉える時は細かい時間刻みが必要となるため、電気角1周期に含まれる計算ステップ数が増加し、結果を得るまでに時間がかかる。
計算時間を短縮する方法として、過渡応答部分の計算をモータの高精度な等価回路モデル(以下、JMAG-RTモデル)による制御・回路解析のみで実施し、定常状態に到達したと判断された段階でFEAモデルに切り替えることが考えられる。
2. 提案手法の課題
JMAG-RTを用いる提案手法を用いた時の総計算量は、JMAG-RTモデル作成時間と制御・回路連成解析の実行時間の合計となる。よって、この合計時間が従来の計算時間に対して短縮される必要がある。
一方、JMAG-RTモデルからFEAモデルに切り替えた時に、JMAG-RTモデルとFEAモデルの鎖交磁束量に整合性が取れない場合、起電圧差が発生して過渡応答が発生する。図1に切り替え計算を行った際に過渡応答が発生した状況を示す。(続く)
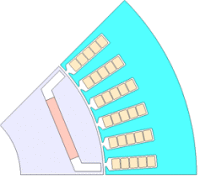
モータ(全体の1/8部分)
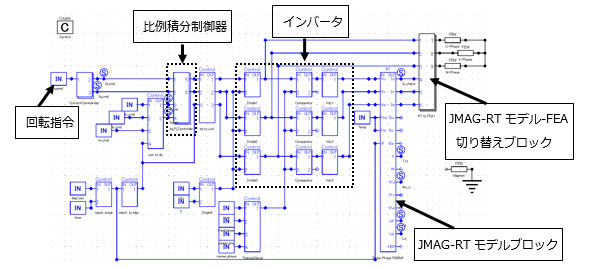
制御回路モデル
回転指令値に応じて動作点を決定し、dq軸電流の指令値を計算する。モータに流れているdq軸電流と指令値を比較し、各相コイルに印加する電圧値を決定する。
『JMAGソフトウェア正規ユーザー(有償会員)』または『JMAG WEB MEMBER(無料会員)』でサインインが必要です。
『JMAG WEB MEMBER(無料会員)』へ登録することで、技術資料やそのほかの会員限定コンテンツを無料で閲覧できます。
登録されていない方は「新規会員登録」ボタンをクリックしてください。



