目次
1. 概要
2. 使用モデル
3. テーブル分解能と精度の関係
3.1. 機械角分解能の依存性
3.2. 電流振幅分解能の依存性
3.3. 電流位相分解能の依存性
4. テーブル分解能と時間分解能が電流精度に及ぼす影響
5. まとめ
6. 参考文献
1. 概要
モータプラントモデルの精度向上のためには空間高調波の考慮が必要である。その精度はプラントモデル生成時の分解能および実行時の時間分解能に強く依存する。
本書ではプラントモデルの一種であるJMAG-RTを用いて、インダクタンスおよび鎖交磁束のテーブルがもつ各軸(機械角、電流振幅、および電流位相)の分解能と精度の関係を示す。加えてJMAG-RT解析実行時の時間刻み幅と精度の関係を示す。
2. 使用モデル
使用するモデルを図1に示す。埋込磁石型永久磁石同期モータであり、その極数は8、スロット数は48である。評価に用いる動作点は低速高トルク、中速中トルク、および高速低トルクの3点とする。それぞれの回転数とトルクを表1に表す。
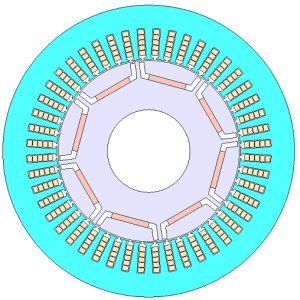
図1 検証用モータの形状
表1 動作点
| 点 | 回転数 rpm | トルク Nm |
| A | 2,000 | 250 |
| B | 3,000 | 140 |
| C | 8,000 | 75 |
3. テーブル分解能と精度の関係
インダクタンスおよび鎖交磁束のテーブルは、機械角、電流振幅、および電流位相の3軸で構成される。本節では、動作点A,B,Cにおいて各軸の分解能を変更し、JMAG-RT実行時の電流値をFEAのそれと比較する(*)。いずれの軸でもFEAとの差が1%以下となる最も分解能の高いテーブルを表2に表す。検討する軸以外の2軸の分解能は表2の設定に従う。また本節においては1ステップあたりの回転角度は0.09deg/stepとする。
表2 高分解能のテーブル
| 軸 | パラメータ |
| 機械角 | 0.5degおき (計91点) |
| 電流振幅 | 5A, 10A, 以降10Aおき300Aまで, 1000A (計32点) |
| 電流位相 | 5degおき (計73点) |
3.1. 機械角分解能の依存性
機械角分解能を22.5deg、7.5deg、0.5degおきと変更したときの電流履歴とFEAとの電流差の履歴を図2に示す。動作点A,B,Cいずれにおいても、分解能が22.5degのときは瞬時の電流差が20%を上回り、精度が不十分であることがわかる。表3および図3にFEAとの電流差の平均を表す。表を見ると、例えば動作点Bでは機械角分解能が0.5degのとき0.5%、7.5degの時1.4%、22.5degのとき26%となる。機械角分解能については極数とスロット数の関係から得られるスロット高調波の周期を10分割程度以上することが望ましい[1]。このモータではスロット高調波の周期は7.5degである。分解能0.5degはそれを15分割しており、妥当であると考えられる。
* : JMAG-RTでは電流制御を行う。最も細かい分解能のテーブルを用いた際に得られた電圧波形をFEAに投入し、その結果をリファレンスとする。第4節も同様。
『JMAGソフトウェア正規ユーザー(有償会員)』または『JMAG WEB MEMBER(無料会員)』でサインインが必要です。
『JMAG WEB MEMBER(無料会員)』へ登録することで、技術資料やそのほかの会員限定コンテンツを無料で閲覧できます。
登録されていない方は「新規会員登録」ボタンをクリックしてください。



