解析屋が見た損失評価

山田　隆

 鉄損は計算できたのですが、モータ屋さんはこれでは満足してくれません。こう聞かれます。”ヒステリシス損失はどのくらい？”、”渦電流損失は？”。正しい質問です。発生原因の異なる損失に分離できれば対策がしやすくなりますから。

 まず、それぞれの損失を定義しましょう。物理現象から定義する立場と式で定義する立場があると思いますが、ここでは計算屋の立場から式で定義していきたいと思います。ヒステリシス損失密度\(P_h\)は周波数\(f\)に比例する成分として次のように定義します。

\( P_h=k_h(B) \times f \quad \cdots \)　(3)

 ここで\( k_h(B) \)は磁束密度に依存した関数で、1周期の間に発生する損失量を表しています。ビジュアルに言えば、渦電流がない場合のBHループの面積です(図4)。これは周波数つまり、磁束密度の変化の速度には依存しません。磁束密度の時間変化がゆっくりでも速くても損失の量は同じです。これは重要な性質なので心に留めておきましょう。例えば、図5の(a)と(b)のように振幅が同じで波形が異っていても対応するBHループは同じになります。ヒステリシス損失は電磁鋼板内の磁壁の移動に伴う損失と言われています<3>。

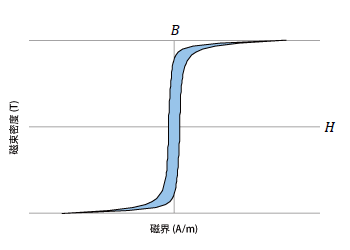図4　BHループ
このBHループの内側の面積がヒステリシス損失に等しい

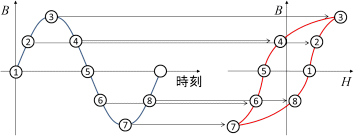(a)正弦波

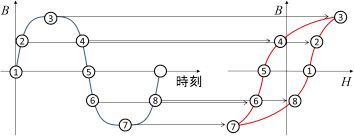(b)台形波
図5　同じヒステリシス損失を与える異なる2つの磁束密度波形

ループ上の各点への到達時間は異なるが軌跡は同じになることに注意

 一方、渦電流損失\( P_e \)は全損失\( P_{tot} \)からヒステリシス損失(3)を差し引いた量として定義します。

\( P_e=P_{tot}-P_h \quad \cdots \)　(4)

 上の定義によれば、ヒステリシス損失を決めている\( k_h(B)\)がわかれば、ヒステリシス損失はもちろん、渦電流損失もわかります。ではどうやって\( k_h(B)\)を求めればよいのでしょうか？手持ちのデータは例の鉄損特性データ\( p(f,B)\)だけです。とりあえず、損失を丁寧に書いてみましょう。

\(\begin{eqnarray} P_{tot} &=& P_h + P_e \\ &=& k_h(B)\times f + P_e \end{eqnarray} \quad \cdots\)　(5)

 (5)式の両辺を\( f \)で割ると、

\( \frac{P_{tot}}{f} = K_h(B) + \frac{P_e}{f} \quad \cdots \)　(6)

 となります。だからどうした、と言わずにぐっと見つめると、\(\frac{P_{tot}}{f}\)は切片\(k_h(B)\)を持ち\(\frac{P_e}{f}\)で変化するfの関数に見えてきます。見えない人は図6を見てください、見えるはずです。つまり、このグラフを作って切片を読み取れば\(k_h(B)\)がわかってヒステリシス損失がわかり、渦電流損失までわかるわけです。

 よーし、と思った方、脇が甘い。切片はfがゼロなので\(\frac{P_{tot}}{f}\)の計算ができません。そこで、どうするかと言えば、ゼロに近い2点、\(f_1\),\(f_2\)での\(\frac{P_{tot}}{f}\)から直線を引いてY軸との交点を\(k_h(B)\)としてしまうのです。

 少々強引な気もしますが世の中そんなものです。ただ、世の中それほど捨てたものでもなくて、実は、\(P_e\)は\(f\)の二乗にほぼ比例することが知られていていて、\( \frac{P_e}{f}\)を直線に置き換えることはそれほど強引なことでもありません。つまり、\(c(B)\)を\(f\)によらない定数として、

\( P_e\) ~ \( c(B) \times f^2 \quad \cdots \)　(7)

であれば、(6)は、

\( \frac{P_{tot}}{f}\) ~ \( k_h(B) + c(B) \times f \quad \cdots \)　(8)

 となり、\(P_{tot}\)は切片\(k_h(B)\)の一次関数で近似できることになります(*1)。近似とはいえ、それ以外に良い方法が思い浮かばないので、それを認めたいと思います。そうは言っても、完全に直線でないことを考えると、精度よく切片を求めるためにはゼロに近い点の値を使った方が良いことはわかると思います(図6)。一方、周波数が極端に低いところで鉄損特性データを測定することは難しいので、通常、50Hz、100Hzあたりの2点を使います。このヒステリシス損失係数の算出方法を二周波法と言います<4>。

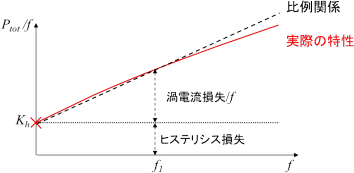図6　二周波法によるヒステリシス損失係数の算出

 例として50A470でやってみましょう。
 図7に示すように、周波数を横軸に、損失を周波数で割った値を縦軸にとるグラフを準備します。
 次に、50 Hz と100 Hzの鉄損特性データを周波数で割った2点をプロットします。図7の点(50, 0.0303)と(100, 0.0371) が該当します。この2点を直線で結び、Y軸との切片を求めます。切片は(0, 0.0235)になりますね。これがヒステリシス損失係数\(K_h\)です。

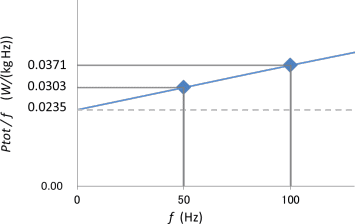図7　50A470のヒステリシス損失係数

 これで、めでたく損失分離ができました。1つ大事なことを忘れていました。上で述べた方法をJMAGで行うためには損失計算の設定の計算オプションで”ヒステリシス損＝FFT、ジュール損＝FFT”とします。この計算オプションが鉄損計算ツールの最初の機能でした(図8)。

図8　アルゴリズム1による損失計算の設定方法

 しかししかし、世の中にはうるさい人がいて、あなたの分離結果を見てこう言うのです。「異常渦電流損失は？」と。い、異常渦電流損失！？大丈夫、説明を忘れていただけです。じつは、この異常渦電流損失というのは曲者で、説明が少々込み入ってくるので、後ほど説明します。

 いよいよ次回は「ヒステリシス損失計算の精度を上げよう！」です。明日をお楽しみに。

1.ただ、(7)と(8)は近似で、その近似度合は材料に大きく依存します。