解析屋が見た損失評価
山田 隆
鉄損計算ツールを1999年にリリースした当時は、飛ぶように売れる、ような状態ではありませんでした。ユーザの反応はいま一つ。”本当に精度が出るんですか?”という疑念に満ちた目で私を見ます。でも、私は気にしません。というのは、上で述べた方法は電気設計では伝統的な方法であり、多くのメーカで使われていた方法であることを知っていたからです。伝統的な方法ではモータ各部の代表値を使って損失を計算するのに対して、JMAGでは各要素にまで分解にして丁寧に計算しています。JMAGの方が良いに決まっています。
それをわかってもらうためにアルゴリズムを説明するわけですが、そうすると、驚いたことに、”その方法は良くないのではないか”という反応が返ってきます。お話を拝聴すると、メーカで使われている方法(またはツール)が信頼性を得ている根拠は、実績であって、アルゴリズムではないのです。確かに伝統的正統派の式が使われているのですが、それぞれの項の前に補正係数なるものがあって、機種毎に経験によって鍛えられた値が存在するのです。叶いません。また、そこは私達のソフトウェアベンダが踏み込むべきところではありません。
アルゴリズムの改良で精度を上げよう!
と、大きく出ましたがどうしましょう?ポイントの1つは損失分離のところで見たヒステリシス損失の性質にあります。ヒステリシス損失の1周期あたりの損失量は周波数によらないことを思い出しましょう (忘れた人は第3話に戻りましょう)。実際、ユーザに突っ込まれたのもその辺りです。
次のような例を考えてみましょう。コイルが巻かれたリングコア(図9)の磁束密度に注目します。
 図9 コイルが巻かれたリングコア
図9 コイルが巻かれたリングコア
コイルに正弦波電流を入れましょう。電流を大きくしていくと磁束密度波形が飽和によって台形波に歪み始めます(図10)。この時の損失を上の”アルゴリズム1″にしたがって計算してみます。
まず、周波数分解するのでしたね。図10の波形を分解すると図11のように複数の周波数成分を持っていることがわかります。その次は、それぞれの周波数について、鉄損特性データを見に行って、磁束密度に対応する損失密度を読み取ります。後は体積をかけて、足し合わせればお仕舞です。
どこがいけないのでしょうか?話をわかりやすくするために、損失はヒステリシス損失だけだと仮定しましょう。
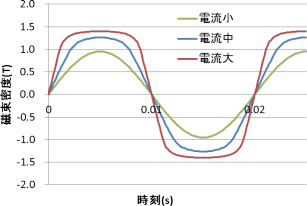 図10 磁気飽和により歪んだ磁束密度波形
図10 磁気飽和により歪んだ磁束密度波形
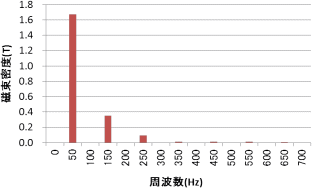 図11 電流大のときの磁束密度の調波分析
図11 電流大のときの磁束密度の調波分析
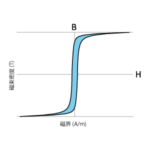
もう一度、台形波を見つめます、そしてこれをBH平面上でどのような軌跡を描くか考えて、いや、考えるよりも描いてみましょう(さぼらずにちゃんと描いてください!)。 そうです、図12のようにループを描くはずです。そして、その面積が損失です。話が見えない?あせらない!
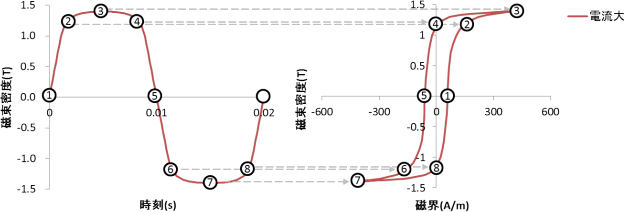 図12 電流大の磁束密度波形(左)とヒステリシスループ(右)
図12 電流大の磁束密度波形(左)とヒステリシスループ(右)
さて、電流の波形をうまく調整して磁束密度の波形が台形波と同じ振幅を持ちつつ、きれいな正弦波にできたとしましょう(図13)。これを同様にBH平面上に描いたらどうなるでしょうか?あら不思議、先ほどのループと同じになります(渦電流がないことをお忘れなく)(図13)。
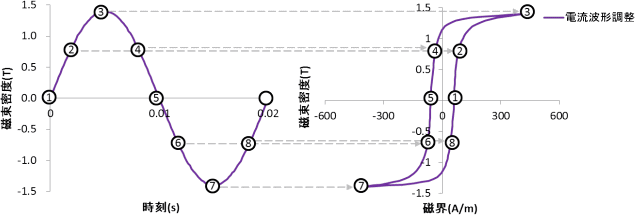 図13 電流波形の磁束密度履歴(左)とそのヒステリシスループ(右)
図13 電流波形の磁束密度履歴(左)とそのヒステリシスループ(右)
つまり、損失は同じです。念のために”アルゴリズム1″で計算すると、台形波の時に現れた高調波分の損失がないことがわかります。あれれ?ですよね (ここで”あれれ”じゃない人、感性高めましょう)。ループ面積から計算すると損失が同じなのに、アルゴリズム1で計算すると損失が異なります。正しいのはループの面積。残念ながらアルゴリズム1は不正解です。
これは、ヒステリシス損失は周波数には依存しない、つまり、磁束密度の変動の速度によらないにも関わらず、それを時間の関数と見てしまったことが誤りでした。
それがわかるとアルゴリズム1など使えない、何でそんなものを紹介したんだ、もっと言えば、製品に組み込んだんだ!と腹が立つかもしれません。落ち着いてください。磁束密度の波形が歪のない正弦波であれば問題がないことを思い出してください。正弦波波形を前提に設計されているモータには有効な方法だったのです。
そうは言っても、今日では強力な永久磁石を使い、流せる限りの電流を投入することが珍しくありません。当然、磁束密度波形は歪んでいます。そうするとアルゴリズム1の分はかなり悪くなります。ヒステリシス損失の計算方法を見直した方がよさそうです。どうしようどうしようと考えていると、素晴らしい手法を提唱されました<5>。ループの数を”数える”方法です (図14)。
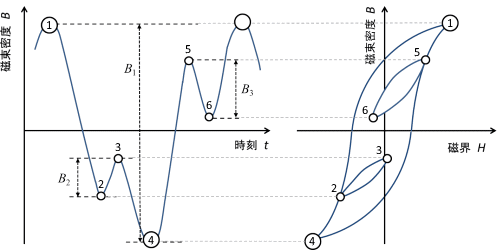 図14 磁束密度波形の極値・振幅(左)とそのヒステリシスループ(右)
図14 磁束密度波形の極値・振幅(左)とそのヒステリシスループ(右)
この方法では磁束密度波形の極値、つまり、振幅の上下の頂点の数を数え、ある極値からスタートして2つめの極値が見つかったらループが1つあったとします。その2つの極値の差をループの振幅\(B_j\)として、鉄損特性データから得られる関数\(k_h(B_j)\)を使って次のようにそのループに対応する損失\(P_j\)を計算します。
\( P_j = \frac{k_h(B_j)}{dt_j} \quad \cdots \) (9)
ここで\(dt_j\)はループ\(j\)の周期で、式(3)
\( P_h=k_h(B) \times f \quad \cdots \) (3)
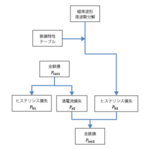
の\(f\)に相当します。これを波形に現れるループの全てについて行い、足し合わせることでヒステリシス損失が計算できます。この方法であれば上で述べた問題は見事に回避できますし、上で見たようにマイナーループも考慮できています。素晴らしい方法です。ヒステリシス損失の計算にはこれを採用させていただくことにしました。これにはアルゴリズム2という名前を付けておきましょう。アルゴリズム2によるJMAGの設定は以下の様になりました (図15)。
図15 アルゴリズム2による損失計算の設定方法
新しい方法を携えて、再度ユーザに説明に向かいました。感触は上々です。ただ、これはJMAGの改良の成果だけではなく、その当時(2000年頃)から急速に損失解析のニーズが高まってきていたこと、さらに大学の研究室で優れた論文が発表され有限要素法による損失解析で良い結果が得られることが示され始めたためだと思います。
いよいよ明日は、第5回・前半の最終回です。