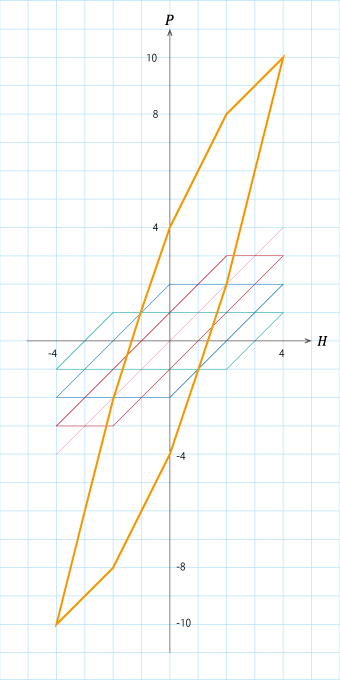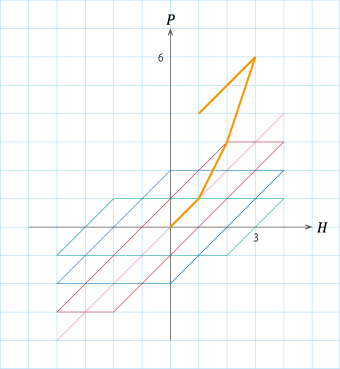解析屋が見た損失評価 夏休み補講編
山田 隆
暑い夏が続いていますね。でも、折角の夏ですからこの暑さを満喫することにしましょう。真冬になればきっとこの暑さが懐かしくなります。人間とは勝手なものです。
さて、今回のお題はプレイモデルです。プレイモデルは新しい損失解析手法としてアルゴリズム3においてヒステリシス損失計算を担っています。プレイモデルがマイナーループを再現できることや、入力としてメジャーループ群が必要なことは述べましたが、そのメカニズムについてはこのコラムではスキップしていました。このメカニズムは少々込み入っていて理解するのに根性がいること、また、利用においては必ずしも内部メカニズムを理解しなくても良いだろうと考えたためです。しかし、先日の次世代セミナーで松尾先生のプレイモデルについてのレクチャー<Ⅰ>を受けた方々から、もう少し勉強したい、とのコメントをいただきましたので、意を決してこのコラムでの説明を試みたいと思います。
ただし、上にも書きましたが、少々根性が必要です。私も頑張りますが、皆さんも頑張ってくださいね。
(01) まずはプレイヒステロン
このくらい脅しておけば10人中9人はすでに脱落して、まだここにとどまっているのは根性のある俊英の方々ばかりでしょうから気が楽です。なーに、実は大したことではありません。少々複雑なだけで、それぞれのステップに難しさはありません。ステップ毎にきちんと理解していけば大丈夫です。
プレイモデルでは、磁界\(H\)に対する磁束密度Bの応答をマイナーループを含めて表現するのですが、あまり焦らずに、プレイモデルの中核となるプレイヒステロンの理解からはじめましょう。プレイヒステロン(以下、ヒステロン)\(p\)は入力された\(H\)に位相遅れを付加する役割を持っており次のように定義されます。
\( p(H,\zeta) = max(min(p_0,H+\zeta),H-\zeta) \quad \cdots \) (S4.1)
ここで\(p_0\)は前のステップの\(p\)の値、\(\zeta\)は量を表現するパラメータです。”位相遅れ”というと仰々しい感じがするかもしれませんが、ヒステリシスループの幅を表していると考えていただければ結構で、\(\zeta\)が大きくなるとヒステリシスループの幅が広がります(*2)。
式S4.1を見ると戦意が喪失してしまうかもしれません。何だかわかりませんよね。自慢ではありませんが、私も最初の一か月間は全く意味不明でした。こういう時には実際に書いてみるのが一番です。 とりあえず、\(\zeta=2\)、\(p_0\)の初期値は0として、\(H\)を0から始めて4まで増やし、そこから引き返して今度は‐3まで行って、また、2まで行きましょうか。 えっ、方眼用紙がない？そんなこともあるかと思って、練習用のマス目(ワークシート)を用意しました。ダウンロードしてお使いください(PDF:20KB)。 どうですか？図S4.1のようひし形になりましたか？何となく、ヒステリシスが見えてきました。 式S4.1の中に前のステップの値\(p_0\)をもつことで、\(p\)がヒステリシス性を持ち、その時点の\(H\)だけではなく、それまでの履歴によることが”感じられ”たと思います。 ここは頭よりも体で習得することが大事です。 練習として表S4.1の\(H\)の変化について\(p\)の履歴を実際に描いてみてください。 答えは図S4.2のようになるはずです。どうですか、合っていましたか?
ヒステロンの基本的な動きが理解できたところで飽和の効果をモデルに持たせましょう。 飽和の効果は一般にいくつかありますが、ヒステロンの役割が\(H\)に位相差を与えることから、ヒステロンが持つ飽和の効果とは”ヒステリシスループを閉じさせる”ことになります。具体的には、対象としている材料が完全に飽和する磁界\(H_s\)(>0)を超えたら\(p\)を一定にしてしまいます。式で書くと
\( p = \begin{eqnarray} \left\{ \begin{array}{l}H_s-\zeta (H \gt H_s) \\ -H_s + \zeta (H\lt-H_s) \end{array} \right.\end{eqnarray}\quad \cdots \) (S4.2)
となります。これは\(H_s\)を越えたところではループを形成せずに閉じた”線”になることを表現しています。この効果を実際に取り込んでみましょう。飽和磁界\(H_s\)を4として、表S4.1の変化に対する\(p\)の履歴を描いてみてください。図S4.3のようになれば正解です。
おっと、大事なことを忘れていました。幅\(\zeta\)がゼロの場合は特別で、\(H_s\)を越えてもそれに無頓着に直線のままです（図S4.4）。屈曲させてはいけません。これは\(\zeta\)がゼロの場合には最初からループは閉じているために上で述べた飽和の効果を入れる余地がないためです。
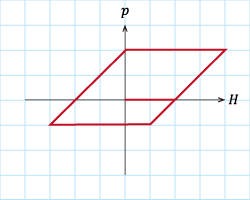図S4.1 \(\zeta=2\)のヒステロン式S4.1の\(p_0\)の値をゼロとして、磁界\(H\)をゼロから始めて1つずつ4まで増やし、そこから-3まで引き返して、再び2まで戻ると、図に示したようなひし形が描ける。
| パターン名 | \(H\)の変化 |
|---|---|
| パターン1 | 0 → 4 → -3 → 2 |
| パターン2 | 0 → 4 → -1 → 4 |
| パターン3 | 0 → -4 → 2 → 0 |
| パターン4 | 0 → 7 → 0 → 4 |
\(H\)の変化パターン例
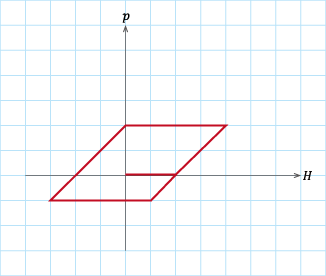(a)パターン1
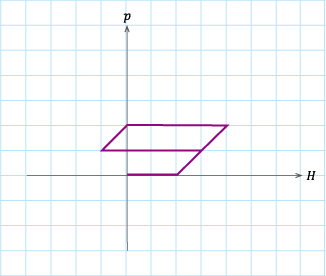(b)パターン2
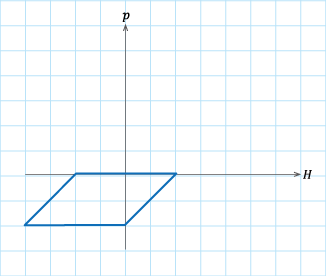(c)パターン3
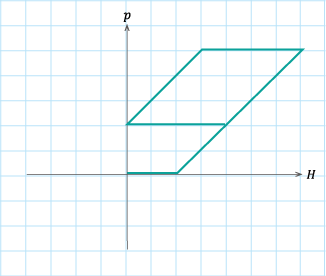(d)パターン4
図S4.2 \(\zeta=2\)のヒステロンの動き
表S4. 1のパターン1からパターン4に従って磁界\(H\)を変化させたときのヒステロンの軌跡。
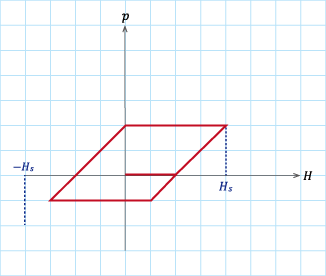(a)パターン1
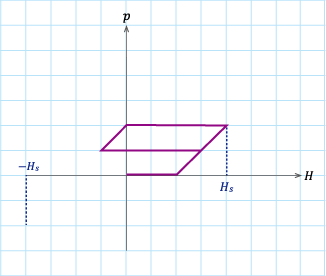(b)パターン2
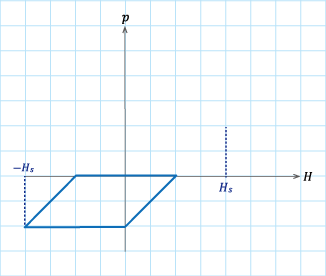(c)パターン3
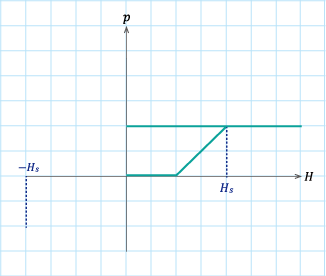(d)パターン4
図S4.3 飽和を考慮した\(\zeta=2\)のヒステロンの動き
表S4. 1のパターン1からパターン4に従って磁界\(H\)を変化させたときの飽和を考慮したヒステロンの軌跡。
図4.2と比較するとパターン4で\(H_s\)を上回った場合に\(p\)が上昇せず一定値となっている。
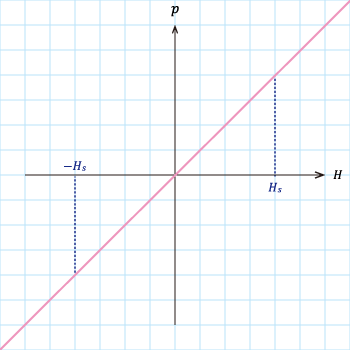図S4.4 \(\zeta=0\)のヒステロン\(\zeta=0\)のヒステロンは飽和磁界\(±H_s\)を越えても直線に伸びる。
(02) ヒステロンを重ねてみる
プレイモデルでは異なる\(\zeta\)を持つ複数のヒステロンを使います。 その\(\zeta\)の値としては原点から\(H_s\)を\(N_p\)に等分割し、その分割点を取ります(図S4.5)。 この分割点\(\zeta\)の上の\(\zeta\)を\(\zeta_n\)とすれば次のように書けます。
\( \zeta = (n-1)*H_s/N_p \quad \cdots \) (S4.3)
分割数\(N_p\)は任意で、\(N_p\)を増やすとマイナーループを捉える分解能が上がりますが、必要なデータ量も増加しますので、実用上は適当なバランスが必要です。 通常は数10程度にします。ただし、図S4.5では簡単のために\(N_p\)を4にしています。なお、\(\zeta\)がゼロのヒステロンも必ず加えます。これも重要な働きをしますので忘れないでください。
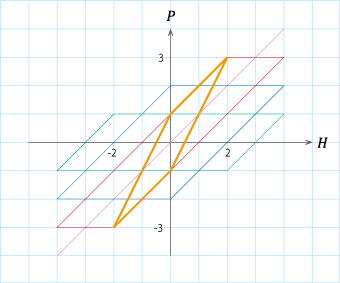
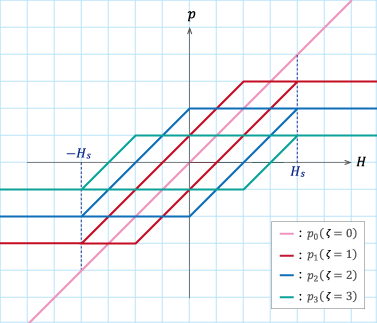図S4.5 4つのヒステロン\(p_0(\zeta=0)\)から\(p_3(\zeta=3)\)を描く。 ここでも飽和磁界\(H_s\)は4とした。
さて、この4つのヒステロンを重ね合わせたらどうなるか見てみましょう、いや、やってみましょう。これもワークシートを準備しましたのでご利用ください(PDF:28KB)。 やることは単純です、4つのヒステロンを足すだけです。すなわち、
\( P(H)= \displaystyle \sum_{n} p_n \quad \cdots \)(S4.4)
ここで、
\( p_n = p(H,\zeta_n) \quad \cdots \)(S4.5)
です。入力の\(H\)を0から4、折り返して‐4、そしてまた、4まで戻してみましょう。 \(P(H)\)はどうなりましたか？正解の軌跡と各点の\(p_n\)の値をそれぞれ図S4.6と表S4.2に載せておきます。 少々ゴツゴツしていますが、何か\(BH\)ループらしい軌跡になっていることがわかると思います。実はこれがメジャーループの”素”になります。
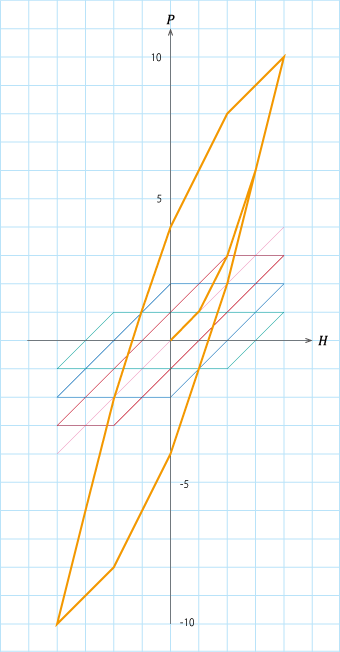図S4.6 ヒステロンの重ねあわせ例(1)4つのヒステロンを用いて\(H\)を\(0 → 4 → -4 → 4\)と変化させた場合の軌跡。
(0,0)から立ち上がり(初磁化に相当)、その後ループを描くことが確認できる(メジャールプールに相当)
| \(H\) | \(p_0\) | \(p_1\) | \(p_2\) | \(p_3\) | \(P(H)\) |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 2 | 2 | 1 | 0 | 0 | 3 |
| 3 | 3 | 2 | 1 | 0 | 6 |
| 4 | 4 | 3 | 2 | 1 | 10 |
| 3 | 3 | 3 | 2 | 1 | 9 |
| 2 | 2 | 3 | 2 | 1 | 8 |
| 1 | 1 | 2 | 2 | 1 | 6 |
| 0 | 0 | 1 | 2 | 1 | 4 |
| -1 | -1 | 0 | 1 | 1 | 1 |
| -2 | -2 | -1 | 0 | 1 | -2 |
| -3 | -3 | -2 | -1 | 0 | -6 |
| -4 | -4 | -3 | -2 | -1 | -10 |
| -3 | -3 | -3 | -2 | -1 | -9 |
| -2 | -2 | -3 | -2 | -1 | -8 |
| -1 | -1 | -2 | -2 | -1 | -6 |
| 0 | 0 | -1 | -2 | -1 | -4 |
| 1 | 1 | 0 | -1 | -1 | -1 |
| 2 | 2 | 1 | 0 | -1 | 2 |
| 3 | 3 | 2 | 1 | 0 | 6 |
| 4 | 4 | 3 | 2 | 1 | 10 |
では、今度は、0から始めて3で折り返して0に戻り、そこでまた折り返して3まで行きましょう。今度はどんな軌跡になったでしょう？正解は図S4.7と表S4.3です。この場合にはマイナーループが描かれています。
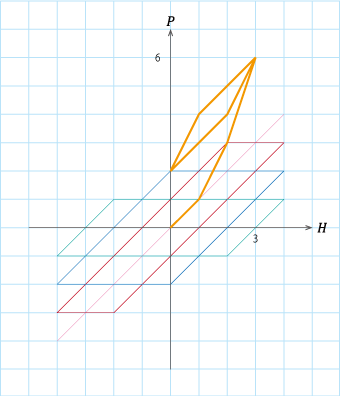図S4.7 ヒステロンの重ねあわせ例(2)4つのヒステロンを用いて\(H\)を\(0 → 3 → 0 → 3\)と変化させた場合の軌跡。 ヒステロンで表現可能な\(H=4\)まで移動せず途中で戻ってもループを描くことが確認できる(マイナーループに相当)
| \(H\) | \(p_0\) | \(p_1\) | \(p_2\) | \(p_3\) | \(P(H)\) |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 2 | 2 | 1 | 0 | 0 | 3 |
| 3 | 3 | 2 | 1 | 0 | 6 |
| 2 | 2 | 2 | 1 | 0 | 5 |
| 1 | 1 | 2 | 1 | 0 | 4 |
| 0 | 0 | 1 | 1 | 0 | 2 |
| 1 | 1 | 1 | 1 | 0 | 3 |
| 2 | 2 | 1 | 1 | 0 | 4 |
| 3 | 3 | 2 | 1 | 0 | 6 |
ああ、素晴らしい！ついにマイナーループを手にしました。冷静に考えればこれは本当のマイナーループではないのですが、感動に水を差すことはやめましょう。本物ではないにせよプレイモデルがマイナーループを描く基本的な要素はここに含まれていますので、この動きが自然に感じられるようになれば、プレイモデル理解の5合目まで来たようなものです。
まだ、動きがしっくりこないという人のために練習問題を3つ用意しておきました。やってみてください。
練習問題
\(p_0\)から\(p_3\)までの4つのヒステロンを使用し問題1から問題3のように磁界\(H\)を変化させたときのプレイモデル\(P_n= p(H,\zeta_n)\)の動きをワークシートに描いてください。
問題1
\(H= 0 → +4 → -4 → +3\)
| \(H\) | \(p_0\) | \(p_1\) | \(p_2\) | \(p_3\) | \(P(H)\) |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 2 | 2 | 1 | 0 | 0 | 3 |
| 3 | 3 | 2 | 1 | 0 | 6 |
| 4 | 4 | 3 | 2 | 1 | 10 |
| 3 | 3 | 3 | 2 | 1 | 9 |
| 2 | 2 | 3 | 2 | 1 | 8 |
| 1 | 1 | 2 | 2 | 1 | 6 |
| 0 | 0 | 1 | 2 | 1 | 4 |
| -1 | -1 | 0 | 1 | 1 | 1 |
| -2 | -2 | -1 | 0 | 1 | -2 |
| -3 | -3 | -2 | -1 | 0 | -6 |
| -4 | -4 | -3 | -2 | -1 | -10 |
| -3 | -3 | -3 | -2 | -1 | -9 |
| -2 | -2 | -3 | -2 | -1 | -8 |
| -1 | -1 | -2 | -2 | -1 | -6 |
| 0 | 0 | -1 | -2 | -1 | -4 |
| 1 | 1 | 0 | -1 | -1 | -1 |
| 2 | 2 | 1 | 0 | -1 | 2 |
| 3 | 3 | 2 | 1 | 0 | 6 |
問題2
\(H= 0 → +3 → +2 → +3\)
| \(H\) | \(p_0\) | \(p_1\) | \(p_2\) | \(p_3\) | \(P(H)\) |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 2 | 2 | 1 | 0 | 0 | 3 |
| 3 | 3 | 2 | 1 | 0 | 6 |
| 2 | 2 | 2 | 1 | 0 | 5 |
| 1 | 1 | 2 | 1 | 0 | 4 |
| 2 | 2 | 2 | 1 | 0 | 5 |
| 3 | 3 | 2 | 1 | 0 | 6 |
問題3
\(H= 0 → +2 → -2 → +2\)
| \(H\) | \(p_0\) | \(p_1\) | \(p_2\) | \(p_3\) | \(P(H)\) |
| 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 2 | 2 | 1 | 0 | 0 | 3 |
| 1 | 1 | 1 | 0 | 0 | 2 |
| 0 | 0 | 1 | 0 | 0 | 1 |
| -1 | -1 | 0 | 0 | 0 | -1 |
| -2 | -2 | -1 | 0 | 0 | -3 |
| -1 | -1 | -1 | 0 | 0 | -2 |
| 0 | 0 | -1 | 0 | 0 | -1 |
| 1 | 1 | 0 | 0 | 0 | 1 |
| 2 | 2 | 1 | 0 | 0 | 3 |
[*1] ”夏休みの宿題”の意味は、私の夏休み中にこれを書くことになっていたからです。でも、夏休み終わっちゃいました。宿題残ってます。この状態、昔から変わりません。ぶれない男です。”少年老い易く学成り難し”。
[*2] 位相遅れという言葉の雰囲気は三角関数で考えるとわかりやすいかもしれません。例えば、\(t\)をパラメータとしたときの、\(xy\)平面上の軌跡、\(x=sin (t), y=sin (t + f)\) において
\(\varphi\)は位相遅れを表し、\(\varphi\)が0のときは軌跡は直線、\(\varphi\)が増えるにしたがって楕円になります。
