解析屋が見た損失評価 夏休み補講編
山田 隆
夏です。暑いです。モータやトランスの損失減らして、少しでも温度下げましょう。そのためにも損失解析を追求せねばいけません。中学生の時、暑い!、と言ったら、夏だから、と言われ、なぜ夏は暑いのだ、と聞いたら、地球の公転軸に対して自転軸が傾いているからだ、と理屈で諭されて、ほー、と思いました。が、だからと言って涼しくなるものでもない。この世の創造主でもない限り地球の自転軸の傾きを変えることはできませんから。でも、モータやトランスなら皆さんが変えられる。素晴らしい。
さてさて、先日までのコラム本編は完全無欠で理解度100%、落ちこぼれゼロを信じて疑わなかったのですが、なぜか、”全然わかんねーぞ”とか”説明甘いんじゃないの”とか、ある意味冷静的確なフィードバックを少なからずいただきましたので、真摯に受け止め、これからしばらくそれらについてお答えしていきたいと思います。
補講第1回:アルゴリズム1とアルゴリズム2の比較
最初は第4話補足の図17についてです。そこでは損失解析の2つのアルゴリズムを使って、リングコアの損失を磁束密度波形が正弦波の場合と台形波の場合について計算してみました。この比較結果をどう理解すればよいか?という問い合わせをいただきました。これについて考えてみましょう。
アルゴリズム1とアルゴリズム2って何だっけ?という人、第2話(アルゴリズム1)、第4話(アルゴリズム2)に戻って復習するのが王道ですが、面倒な人は第4話補足の図16と第9話の表3くらいは確認しましょう。それも面倒な人、しょうがないですね、両者の違いはヒステリシス損失の計算方法にあってアルゴリズム2の方が改良版で歪波形に対して適応力が高いことくらいは覚えておいてください。
図17を眺めてみましょう。まず、アルゴリズムや波形によらず周波数が高くなるにつれて渦電流損失の割合が高くなっていることに気が付くと思います。これは、ヒステリシス損失が周波数に比例するのに対して、渦電流損失は周波数の”ほぼ”二乗に比例するためですね。ここで”ほぼ”としたのは、表皮効果や異常渦電流損失の影響があるためです。
では、アルゴリズム間の違いを探ってみましょう。一番わかりやすいのは図17(a)の50Hzの結果です。ヒステリシス損失がアルゴリズムによって異なっています。そもそも、アルゴリズム2は歪んだ波形を扱えるようにするために導入した方法ですから、異なっていてもらわないと困るのですが、もう少し丁寧に見てみましょう。コア中央部における磁束密度波形を図S1.1に、それの周波数分解の結果を図S1.2に示します。
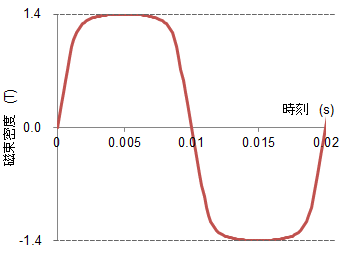 図S1.1 磁束密度波形(台形波:50Hz)
図S1.1 磁束密度波形(台形波:50Hz)第4話の図10にも示したように励磁電流が大きい場合、磁気飽和の影響で磁束密度波形が台形波になっている。
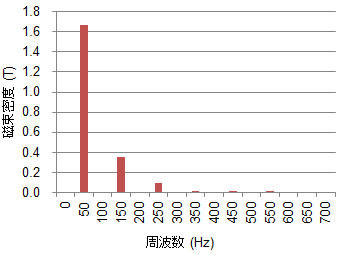 図S1.2 磁束密度波形(台形波:50Hz)の調波分析
図S1.2 磁束密度波形(台形波:50Hz)の調波分析図S1.1に示した磁束密度波形(台形波:50Hz)に対して調波分析を行った結果、基本周波数50Hzで大きな磁束密度成分が確認できるだけでなく、3次(150Hz)、5次(250Hz)においても有意な成分が確認できる。
アルゴリズム1ではヒステリシス損失の計算にも周波数分解の結果を使い、次のように計算します。
\( P_h = \displaystyle \sum_{l}k_h (B_i) \times f_i \quad \cdots \) (S1.1)
ここで\(f_i\)は第\(i\)次の周波数、\(B_i\)は第i次の磁束密度振幅です。また、\(k_h(B_i)\)は磁束密度\(B_i\)の時のヒステリシス損失係数で、これは電磁鋼板の鉄損特性(第2話の図2)から二周波法(第3話)によって算出できます。今回のケースに諸量を表S1.1にまとめます。第4話でも述べたとおり、ヒステリシス損失の現象は周波数にはよらないため、上のような周波数分解に基づく方法は正弦波から歪んだ波形の場合には誤差を多く含み、一般的に、高調波成分によって過大評価になってしまいます。
一方、改良版であるアルゴリズム2では、周波数分解をせずに、波形に現れる極値から\(BH\)ループの磁束密度振幅を算出し、その磁束密度振幅を使って、鉄損特性からヒステリシス損失係数を求めヒステリシス損失を計算します(式(9))。
\(p_j = \frac{k_h(B_j)}{dt_j}\quad \cdots \) (9)
今回の場合、凸凹のない台形波のためマイナーループはなく、メジャーループ1つになります。アルゴリズム2についても諸量を表S1.2にまとめます。
いかがでしょうか、台形波の場合にアルゴリズムによって差が出る理由を理解していただけたでしょうか。それが理解できていれば正弦波の場合に差が出ないことも理解できると思います。念のために正弦波についても波形、周波数分解結果および表S1.1、表S1.2に対応する計算過程の諸量を図S1.3、図S1.4、表S1.3、表S1.4にまとめておきます。正弦波では高調波成分がないために差が出ないことがわかります。
ちなみに、渦電流損失については両者とも全く同じ結果になっていますが、これは計算の手続きが同一なためです(第4話補足の図16)。
明日はアルゴリズム3の結果について説明を加えたいと思います。
| \( f\) (Hz) | 50 | 150 | 250 | トータル \(P_h\) |
| \( B\) (T) | 1.6705 | 0.3503 | 0.0957 | – |
| \( k_h\) | 0.0520 | 0.0039 | 0.0003 | – |
| \( k_h \times f\) | 2.6000 | 0.5903 | 0.0866 | 3.2768 |
図S1.2で得られた調波分析結果から、図2の鉄損特性に対してアルゴリズム1を利用して、各磁束密度の値に対応するヒステリシス損失係数を求める。ヒステリシス損失係数に各周波数を乗じ、全周波数で足し合わせることでヒステリシス損失Phを求める。トータルのヒステリシス損失3.2768Wは第4話補足図17(a)、50Hz、アルゴリズム1のヒステリシス損失の値である。
| \(1 / dt\) (Hz) | 50 | トータル \(P_h\) |
| \(B\) (T) | 1.4000 | – |
| \(k_h\) | 0.0384 | – |
| \(k_h / dt\) | 1.9205 | 1.9205 |
図S1.1の磁束密度波形から振幅1.4Tを参照し、アルゴリズム2を利用してヒステリシス損失係数を求める。ヒステリシス損失係数に周波数50Hzを乗じた値がそのままトータルのヒステリシス損失Phになる。求められた1.9205Wは第4話補足図17(a)、50Hz、アルゴリズム2のヒステリシス損失の値である。
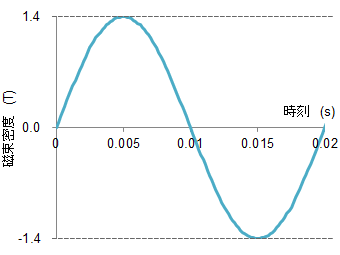 図S1.3 磁束密度波形(正弦波:50Hz)
図S1.3 磁束密度波形(正弦波:50Hz)第4話の図13にも示したように、磁束密度の振幅が図S1.1の波形と同じく1.4Tになるようにコントロールされた正弦波の磁束密度波形を示す。
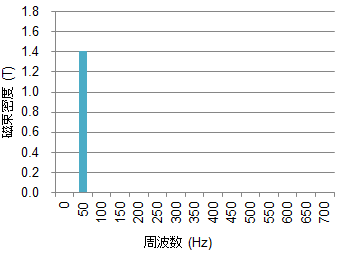 図S1.4 磁束密度波形(正弦波:50Hz)の調波分析
図S1.4 磁束密度波形(正弦波:50Hz)の調波分析図S1.3に示した磁束密度波形(正弦波:50Hz)に対して調波分析を行った結果、基本周波数50Hzでのみ磁束密度成分(振幅の1.4T)をもつことが確認できる。
| \(f\) (Hz) | 50 | 150 | 250 | トータル \(P_h\) |
| \(B\) (T) | 1.4000 | 0.0000 | 0.0000 | – |
| \(k_h\) | 0.0384 | 0.0000 | 0.0000 | – |
| \(k_h \times f\) | 1.9205 | 0.0000 | 0.0000 | 1.9205 |
図S1.4で得られた調波分析結果から、図2の鉄損特性に対してアルゴリズム1を利用して、各磁束密度の値に対応するヒステリシス損失係数を求める。50Hzのみ磁束密度成分があるため、ヒステリシス損失係数に50Hzを乗じて、ヒステリシス損失Phを求める。トータルのヒステリシス損失1.9205Wは第4話補足図17(b)、50Hz、アルゴリズム1のヒステリシス損失の値である。
| \(1 / dt\) (Hz) | 50 | トータル \(P_h\) |
| \(B\) (T) | 1.4000 | – |
| \(k_h\) | 0.0384 | – |
| \(k_h / dt\) | 1.9205 | 1.9205 |
図S1.3の磁束密度波形から振幅1.4Tを参照し、アルゴリズム2を利用してヒステリシス損失係数を求める。ヒステリシス損失係数に周波数50Hzを乗じた値がそのままトータルのヒステリシス損失Phになる。求められた1.9205Wは第4話補足図17(b)、50Hz、アルゴリズム2のヒステリシス損失の値である。