解析屋が見た損失評価 夏休み補講編
山田 隆
(13) プライザッハモデルとプレイモデル(上)
前回の最後で”本番はこれからだ!”とすごんで見せましたが、すみません、言い過ぎました。それ程大層な話ではありません。ただ、プレイモデルとプライザッハモデルの関係について述べることがプライザッハモデルに踏み込んだ目的でしたから、それを忘れるわけにはいきません。
冒頭でもお話しした通り、プレイモデルの説明はプライザッハモデルを基にして行われることが多く、それがとても重要なのにも関わらず、多くの解説では非常にあっさりと天才的に書かれており、凡才で”数式”よりも”絵”、”厳密性”よりも”肌感”を好む私は[*1] 、それを理解するためにのたうち回るような苦しみを味わいました。私も極めて平均的な日本人ですので、同様の性向を持つ人もいないとも限らず、そういう人たちにとって、もう少し別の説明があっても邪魔にはならないだろうと思い、ここではそれにチャレンジしてみたいと思います。
最初に、両者の関係を端的に述べてしまえば、両者は等価である、つまり、同じものだ、というのが結論です。もちろん、計算方法やデータの持ち方などは違いますが、その意味するところ、表現能力などは同じだということです。その等価性の説明は数式を使ってきれいに示されているのですが<Ⅱ>、何かしっくりきません。そこをもう少し何とかしたいと思います。
ヒステロンと磁気モーメントの関係
もし、両者が同じであれば言い換えができるはずです。ということで、プレイモデルのヒステロンをプライザッハモデルを使って表してみましょう。尚、両者の出力の単位を揃えるために、ヒステロンの出力には\(B\)への単位変換だけする形状関数が作用しているとします。また、若干抵抗はあるかもしれませんが、磁気モーメントの出力も\(B\)とします。また、両モデル内での分割数\(N_p\)および\(N_q\)を同じにし、ここでは簡単のために\(N_p=N_q=4\)とします。
まず最初に幅がゼロのヒステロン(\(p_0\))について考えます。このヒステロンの特徴は行きも帰りも同じ線上を動くことですね。これをプライザッハモデルの磁気モーメントで表そうとすると\(H_u\)と\(H_v\)が同じ、つまり、\(H\)の上昇時も下降時も同じタイミングで反転する磁気モーメントが使えそうです。しかし、磁気モーメントが1つだけだとある\(H\)でしか反転が起こらず、ヒステロンの振る舞いが再現できません(図S4.28)。ならば、ということで反転タイミングが異なる\(H_u=H_v\)の磁気モーメントを増やしていくと大分良い感じになってきました(図S4.29)。この磁気モーメントを\(H_u-H_v\)グラフ上で見てみると、当たり前ですが、\(H_u=H_v\)を満たす線上にきれいに並びます。だからどうした、と言わずに、今度は、ヒステロン\(p_1(\zeta=H_s/N_p)\)について考えてみましょう(図S4.30)。この場合は、\(H_u\)と\(H_v\)の差が\(2\zeta(=2H_s/N_p)\)になる磁気モーメントを並べるとヒステロンが再現できて、\(H_u-H_v\)グラフで見ると\(p_0\)に対応した格子の1つ右下の列が\(p_1\)に対応していることがわかります。何となく見えてきました。同じことを\(p_2\)、\(p_3\)、、、と続けていくと順次、斜めの列に対応していることが確認できます(図S4.31)。つまり、それぞれの列がヒステロンで、\(H_u-H_v\)グラフの上にヒステロンを描くことができたわけです。
\(p-\zeta\)グラフの導入
プレイモデルで説明した時のヒステロンは、\(p-H\)平面上に描いていたのでひし形でしたが、\(H_u-H_v\)グラフの上では各ヒステロンはただの”棒”のような姿になってしまいます。それでもヒステロンはヒステロンです。ヒステロンの動きをしていることを確認しておきましょう。まず、動作範囲ですが、上の磁気モーメントとの対応を考えると、それぞれの列の長手方向の中央でヒステロンは0で、\(H_u=H_s\)または\(H_v=-H_s\)では、それぞれ次の式で計算されるヒステロンの最大値\(p_n max\)または最小値\(p_n min\)をとることがわかります(図S4.32)。
\( p_nmax = H_s – \zeta_n, p_nmin = -H_s +\zeta_n \quad \cdots \) (S4.29)
ところで、図S4.32(b)を眺めていると、無性に\(p\)と\(\zeta\)の座標軸を入れたくなりますよね。ここは是非そう思っていただいて、図4.33のように\(H_u-H_v\)グラフに\(p-\zeta\)の座標軸を重ねます。この\(p-\zeta\)グラフはプレイモデルではプライザッハモデルの\(H_u-H_v\)グラフに相当する重要なツールになります。
今日は\(p-\zeta\)グラフを手に入れたところで一休みしたいと思います。次回は\(p-\zeta\)グラフを使ってプレイモデルとプライザッハモデルの関係を見ていきます。
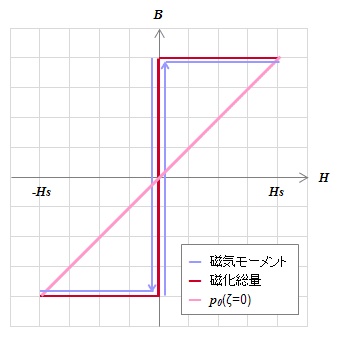 図S4.28 1つの磁気モーメントとヒステロン\(p_0\)
図S4.28 1つの磁気モーメントとヒステロン\(p_0\)\(H_u=H_v\)の1つの磁気モーメントによる磁化総量とヒステロン\(p_0\)を描く。
 (a)
(a)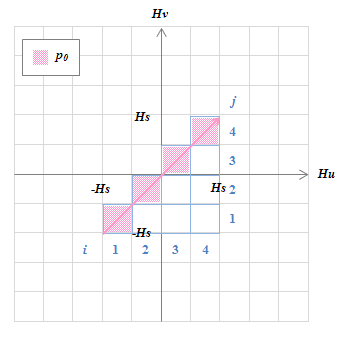 (b)
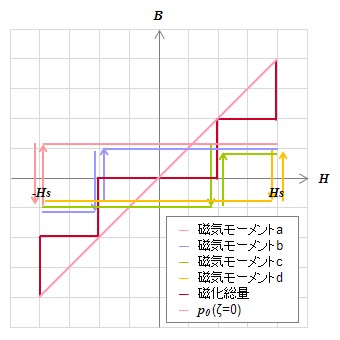
(b)\(H_u=H_v\)の4つの磁気モーメントによる磁化総量とヒステロン\(p_0\)を描く。(左図(a))
\(H_u-H_v\)グラフ上に(a)で得られた\(p_0\)を描く。(右図(b))
 (a)
(a)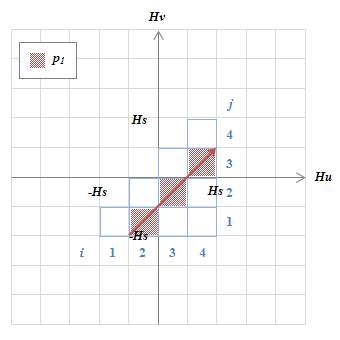 (b)
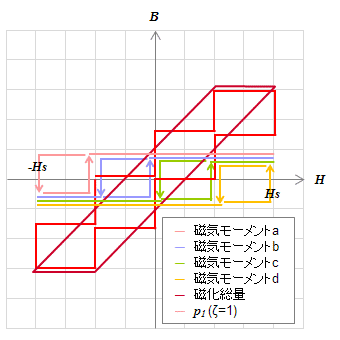
(b)\(2\zeta(=2H_s/4)\)の4つの磁気モーメントによる磁化総量とヒステロン\(p_1\)を描く。(左図(a))
\(H_u-H_v\)グラフ上に(a)で得られた\(p_1\)を描く。(右図(b))
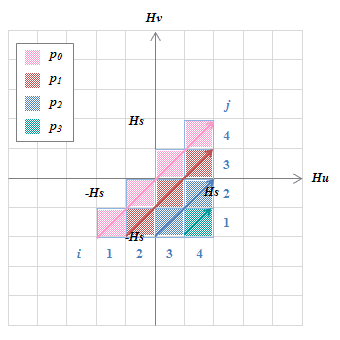 図S4.31 \(H_u-H_v\)グラフ上の4つのヒステロン
図S4.31 \(H_u-H_v\)グラフ上の4つのヒステロン図S4.29、S4.30の手順に従い\(H_u-H_v\)グラフ上に\(p_2, p_3\)まで描く。
 (a)
(a)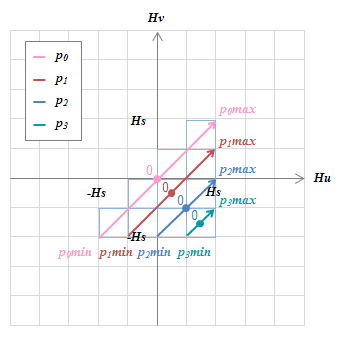 (b)
(b)4つのヒステロンを描く。(左図(a))
\(H_u-H_v\)グラフ上に\(p_0\)から\(p_3\)それぞれのヒステロンの最大、最小、ゼロを描く。(右図(b))
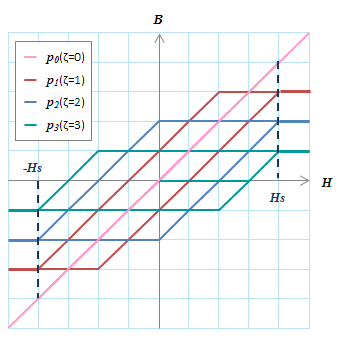
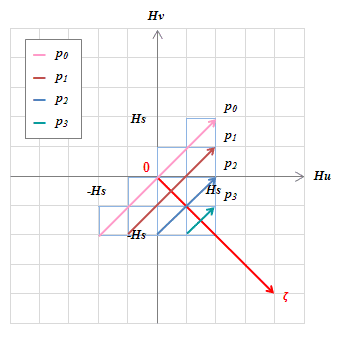 図S4.33 \(H_u-H_v\)グラフと\(p-\zeta\)グラフの重ね合わせ
図S4.33 \(H_u-H_v\)グラフと\(p-\zeta\)グラフの重ね合わせ\(H_u-H_v\)グラフに図S4.32のヒステロンの軸と各ヒステロンのゼロを結んだ\(\zeta\)軸を描く。
[*1] ちなみに焼酎は麦よりも芋です。