解析屋が見た損失評価 夏休み補講編
山田 隆
プレイモデルでもう十分、お腹いっぱい、もう食べられません、という人もいるかもしれませんが、ここはなんとしてももうひと頑張りしていただきたいと思います。というのは、プレイモデルの解説や議論はプライザッハモデルを基にされることが多く、殆どの、もっと言えば私が知る限りの全ての解説はプライザッハモデルの理解を前提にされており、それらの文献で勉強したり、議論に参加する際にプライザッハモデルの理解は大事なのです。プレイモデルはプライザッハモデルと数学的には等価であり、プライザッハモデルの方が物理的なイメージを与えやすく歴史もあることなどから、プライザッハモデルを基礎としたプレイモデルの説明が主流になっているのだと思います。
だったらなぜこのコラムでも、最初からプライザッハモデルを使って説明しなかったのだ、と叱られそうですが、その手順で説明するのであれば、世の中にある高名な先生方の論文の紹介以上にできることはなく、それに、プライザッハモデルによらない説明が1つくらいあっても悪くないかと・・・。実際、私はその正道に挑戦したのですが、最初はプライザッハの山を越えたところで力尽きてしまい、プレイモデルにたどり着けませんでした。そのときつくづく、プレイモデルだけで説明してくれないかなぁ、と思ったものです。
ただ、プライザッハモデルを理解することは、今後の勉強を進めるうえで有益ですし、何よりもプライザッハモデルを通してプレイモデルを見直すことでその理解も深まるのではないかと思います。それでは、プライザッハモデルの説明から始めましょう。
(09) プライザッハモデルの原理
プライザッハモデルもプレイモデル同様、任意のマイナーループを表現するための磁化モデルです<Ⅰ,Ⅱ>。 プライザッハモデルでは、磁化特性は磁化反転の特性が異なる磁気モーメントの足し合わせで表現します。 それぞれの磁気モーメントの状態は正方向または負方向に完全に磁化された2つの状態(+1/2または-1/2)しかありません。
\(H = H_u\)で正方向に完全に磁化(+1/2)され、\(H = H_v\)で負方向に完全に磁化(‐1/2)されます。 これを図に描くと図S4.21のような幅\((=H_u-H_v)\)を持つループになります。ここでのポイントは磁気モーメントが2つのパラメータ\((H_u,H_v)\)で完全に特徴づけられることです。
このような磁気モーメントの組み合わせでどの様な磁化状態が作られるか見てみましょう。 簡単のために図S4.22の(a)のように3つの磁気モーメント\(a,b,c\)がある場合を考えましょう[*1]。 注目するのは磁気モーメントの総和です。初期状態としてすべての磁気モーメントが(-1/2)であるとします。この時の磁化総量は‐3/2ですね。 この状態で磁界を\(-H_s\)から\(H_s\)まで増加させて行くと\(H_{ua}\)で磁気モーメント\(a\)が+1/2に反転し、続いて\(H_b\)および\(H_c\)でもbおよびcでも反転が起こります。 ここでの総量は+3/2です[*2]。今度は\(H=0\)まで減少させます。 そうすると、\(H_{vc}\)を通過した時点で磁気モーメント\(c\)のみが-1/2に反転し、総量は(+1/2)になります。ここで再度\(H\)も通過しますが、磁気モーメント\(b\)は既に+1/2なので何も起こりません。 総量の軌跡を見てみるとマイナーループのようなものが作られているのがわかると思います。
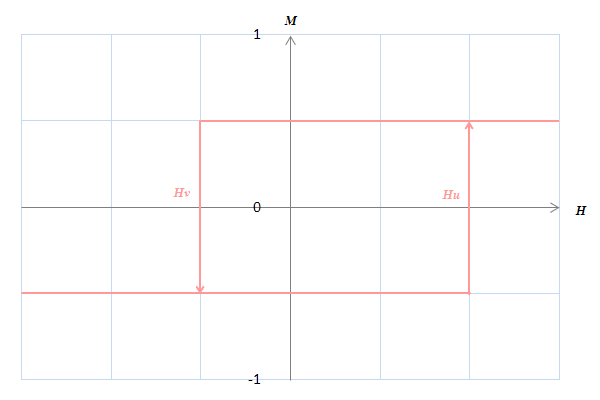 図S4.21 プライザッハモデルで使われる磁気モーメント
図S4.21 プライザッハモデルで使われる磁気モーメント磁気モーメントは\(H_u\)と\(H_v\)によって特徴づけられる
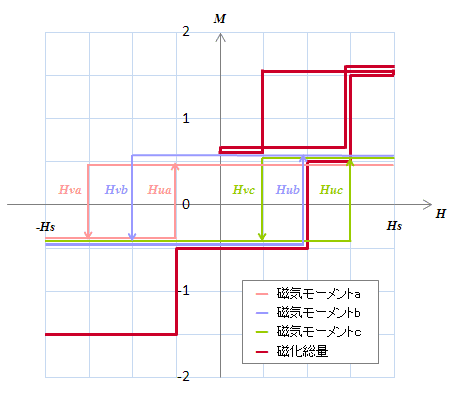 (a)
(a)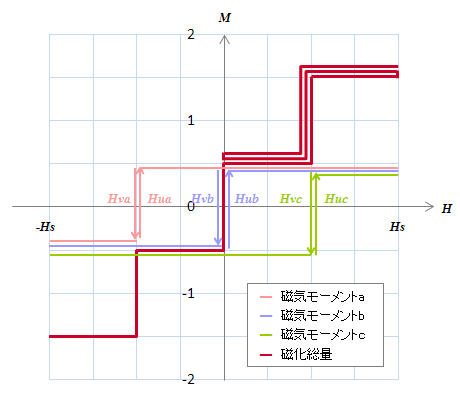 (b)
(b)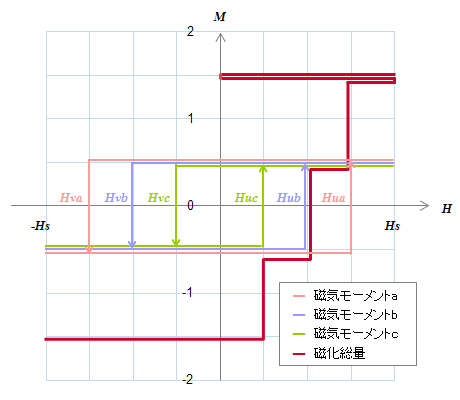 (c)
(c)同じ入力\((-H_s→H_s→0→H_s)\)でも磁気モーメントの組み合わせによって出力が変わる。
(10) \(H_u-H_v\)グラフで考える
この例では、磁気モーメントの数が3つしかないために、磁化の変化がガタガタしてしまっていますが、これは磁気モーメントの数を増やすことでスムースにすることができますので、このガタガタにはしばらく目をつぶっていてください。各磁気モーメントの幅や位置、すなわち、\((H_u, H_v)\)を変えた場合の様子を図S4.23に示します。同じ入力に対して磁化総量の応答が各磁気モーメントの\((H_u, H_v)\)によって変わることはわかります。このことから、材料の特性はいろいろな\((H_u, H_v)\)を持つ磁気モーメントを適切に組み合わせることで表現できることがわかると思います。
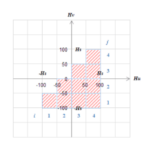
この組み合わせの様子を把握するためにプライザッハモデルでは図S4.23のような\(H_u-H_v\)グラフを使います。グラフ平面は正方格子状になるように各軸上で等分割されています。この分割数を\(N_q\)としましょう。 分割数\(N_q\)は任意で、分割数を増やすほどモデルの分解能\((ΔH=2H_s/N_q)\)も上がりますが、必要なデータ量も増えますので注意が必要です。 ここでは\(N_q=8\)としています。このグラフ上の1つの格子\((i,j)\)が対応する\((H_u, H_v)\)を持つ磁気モーメントを表します(\(i,j\)はそれぞれ\(H_u\)、\(H_v\)軸上での分割番号)。 印加された磁界方向に反転することを前提とすれば\(H_u>H_v\)の条件が課され、\(|H|>H_s\) の動きは自明であることから、検討対象の範囲は図S4.23の右下の三角形の領域になります。 上の例で使ったそれぞれのケースの磁気モーメントはどこに配置されるでしょうか?考えてみてください。
次回は磁気モーメントから実際の磁化特性を\(H_u-H_v\)グラフを使って計算する方法について説明します。
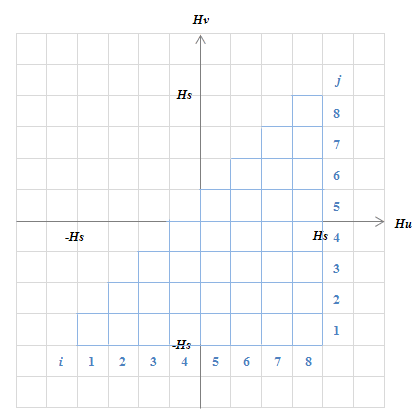 図S4.23 \(H_u-H_v\)グラフ(\(N_q=8\)の場合)
図S4.23 \(H_u-H_v\)グラフ(\(N_q=8\)の場合)格子の1つ1つが異なる特性を持つ磁気モーメントを表している。
磁気モーメントは右下半分の三角形領域内に存在する。
格子番号は\((i,j)\)で表記され、最左下の格子は(1,1)となる。
[*1] 磁化状態の正負の対称性を確保するために\(H_{va}=-H_{uc}\)、\(H_{ua}=-H_{vc}\)、 \(H_{ub}=-H_{vb}\)としています。この対称性は常に利用します。
[*2] 1つの磁化の反転で-1/2から+1/2へ変化するので、変化総量は1になります。