解析屋が見た損失評価 夏休み補講編
山田 隆
(13) プレイモデルの動き、プライザッハモデルの動き(下)
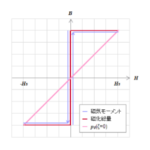
前回は\(H_u-H_v\)グラフ上にヒステロンを描き\(p-\zeta\)グラフを導入しました。 今回はその動きを見てみましょう。 準備として\(H\)を\(H_s\)を通るメジャーループに乗せ\(-H_s\)に持ってきます。ここをスタートポイントにします。 ここから\(H\)を\(-H_s→+H_s→0→+H_s\)と動かします。この時の各ヒステロンの動きと値をそれぞれ図S4.34と表S4.7に示します。ここまでは復習です。新しいことは何もありません。 わからん、という人はお問い合わせください。さて、表S4.7のヒステロンの動きを上で準備した\(p-\zeta\)グラフの上に描くと図S4.35のようになります。 ふーん、という感じですが、とりあえず、これはこれで置いておきましょう。後で戻ってきます。
今度は上の動きをプライザッハモデル、つまり、\(H_u-H_v\)グラフで見てみましょう。 これは最近やったばかりですね(図S4.27参照)。 このプライザッハモデルの動きと上のヒステロンの動き(図S4.34)をじーっと見比べると、各ヒステロンの先端を結んだ線と磁気モーメントの反転のフロントラインが重なっていることがわかります。 つまり、プライザッハモデルの動きはプレイモデルの動きと同じであることがわかります。 逆に言えば、ヒステロンの動きはプライザッハモデルの磁気モーメントの反転の様子を表していると言うこともできるわけです。
形状関数と分布関数の関係は？
上で述べたプレイモデルおよびプライザッハモデルの動きは、それぞれヒステロン{\(p_n\)}および磁化状態を表す{\(D(i,j)\)}で表現され、それらは同じ働きをすることを見てきたわけですが、それでは、プレイモデルの形状関数{\(f_n\)}とプライザッハモデルの分布関数{\(K(i,j)\)}の関係はどうでしょうか?実は、これも等価な関係にあります。ただ、形状関数そのものではなく、形状関数の差分\(\mu(n,m)*Δp\)と分布関数\(K\)が同じです。これはそれぞれの導出手順を思い出していただければわかりやすいと思います。 プレイモデルでは式(S4.15)～式(S4.19)、プライザッハでは式(S4.25)～(S4.28)を見れば同じ操作であり、かつ、計算対象は図S4.34を見ると同じ個所の値を求めていることがわかります。 それはプレイモデルの同定に使った表S4.4を45度傾けて見ると、プライザッハの分布関数表と同じになることを見ても確認できます(図S4.36)。
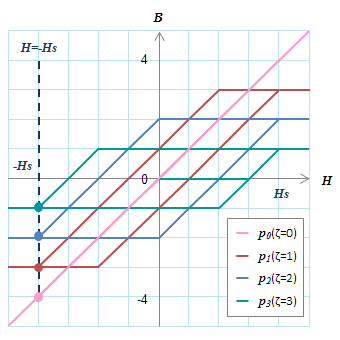(a) \(H=-H_s\)
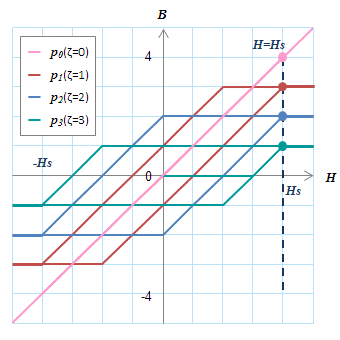(b) \(H=+H_s\)
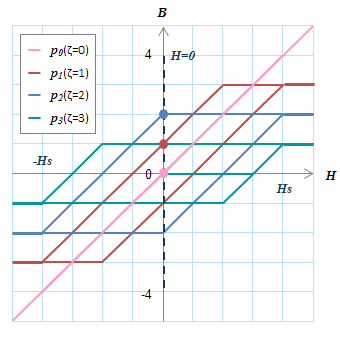(c) \(H=0\)
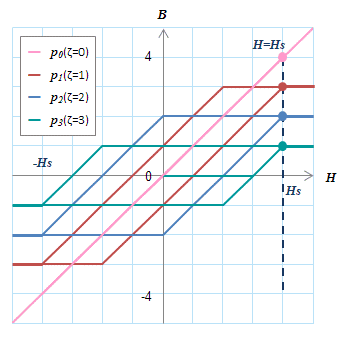(d) \(H=+H_s\)各動作点上に縦線を引き(点線)、各ヒステロンとの交点をとることで値を求めることができる。
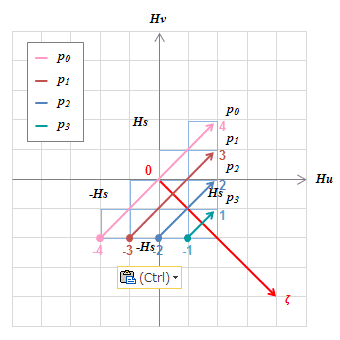(a) \(H=-H_s\)
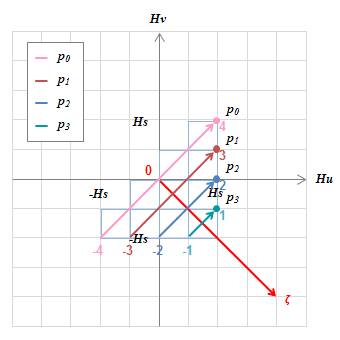(b) \(H=+H_s\)
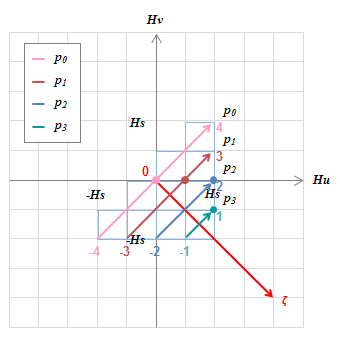(c) \(H=0\)
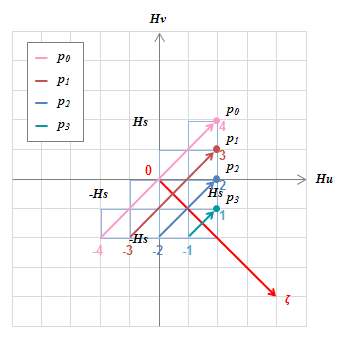(d) \(H=+H_s\)図S4.34もしくは表S4.7で得られた各動作点でのヒステロンの値を\(H_u-H_v\)グラフの\(p\)軸にプロットしていく。
p軸は式(S4.29)が示すように左端が\(p_nmin\)、右端が\(p_nmax\)、中点が0となる。
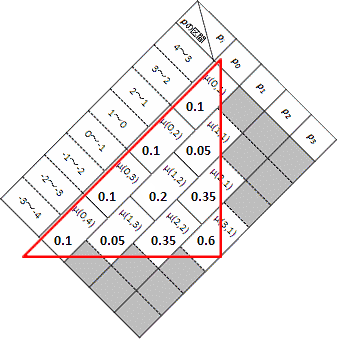(a)
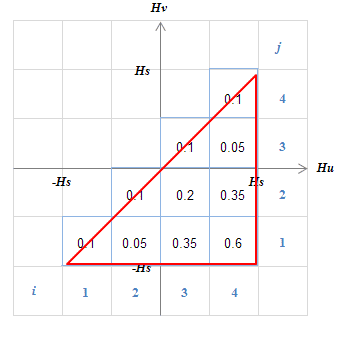(b)表S4.4の行はヒステロンの値、列はヒステロンを表しているので、\(p-\zeta\)グラフとの対応が可能になる。
\(p-\zeta\)グラフはプライザッハの分布関数表と対応づけされているので
結果プレイモデルの同定結果とプライザッハの分布関数の対応づけが可能になる。
視覚的にも表S4.4を45度回転させると升目ごとに対応づけができる。
お疲れ様でした！
プレイモデルとプライザッハモデルが、仕組みは違うものの、同じ働きをすることをご理解いただけたでしょうか。その理解を基にプレイモデルをもう一度プライザッハモデルから見直してみると、より理解も深まると思います。もしかしたら、次々と疑問を生むパンドラの箱を開けることになってしまうかもしれませんが。
さて、これでプレイモデルのお話もおしまいです。冒頭にもお話しした通り、プレイモデルは難しくはないのですが、登場人物が多いので物語全体の意味を把握するには少し我慢が必要です。私は当たり前と思うことでも手を動かして確認していくことをお勧めします。そして、よくわからないこと、おかしいぞ、と思うことがあればお問い合わせをいただければと思います。
損失解析の解説の補講のつもりで始めたこのシリーズも予定よりも大分長くなってしまいました。お付き合いいただきありがとうございました。気がつくと秋の気配が漂っています。
