解析屋が見た損失評価 夏休み補講編
山田 隆
昨日までの疑問点は良く理解できたでしょうか？単純なリングコアのモデルですが現象はそれほど単純ではありません。損失解析は侮れません。では、引き続き、残りの疑問点の解消に向かいましょう。
Q3：なぜ直流重畳がある場合、高周波域で渦電流損失が高いのか？(ケースDH)
ケースDHの渦電流損失を見ると、アルゴリズム2に対してアルゴリズム3の結果が1.7倍大きくなっていることがわかります。これはアルゴリズム3では表皮効果に伴う磁気飽和の影響をより正確に取り込むことができているためです。
表皮効果によって磁束密度が表面に集中する様子は先のQ2でも見てきました。それに伴って磁気飽和が起こり、表面付近の透磁率が低下し、表皮層が深くなります。結果として、より多くの電流が流れ、損失が上昇します。アルゴリズム2では、この現象を捉えることができません。
もう少し具体的に見てみましょう。まず、磁界解析で得られる磁束密度波形は図S3.1のようになります。アルゴリズム2では、これを周波数分解します(図S3.2)。
そして、各周波数毎に磁束密度振幅に応じた損失値を鉄損特性から取得します。つまり、実際には直流重畳によって動作点が1Tを超える高磁束密度域にあるわけですが、アルゴリズム2ではその”記憶”は消去され、ゼロを中心とした動作点での交流場として扱われてしまいます[*1] 。
この動作点の移動がどのような誤差を生み出すか見るために、本来の動作点(図S3.1)と動作点をゼロ中心にした場合(図S3.1から直流成分を差し引いたもの)での鋼鈑内での磁束密度と渦電流損失密度の分布を図S3.3 に示します。動作点をゼロ中心に移動することによって、飽和の影響が少なくなるために表皮層が浅くなり、つまり、渦電流が抑制され渦電流損失が減少することがわかります。この減少分がアルゴリズム2の誤差になります。
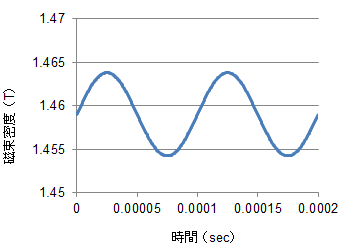図S3.1 ケースDHの磁束密度波形
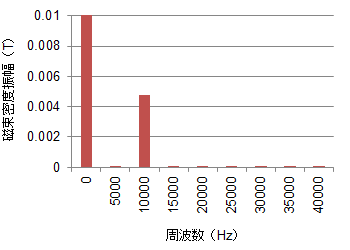図S3.2 ケースDHの磁束密度波形の周波数分解
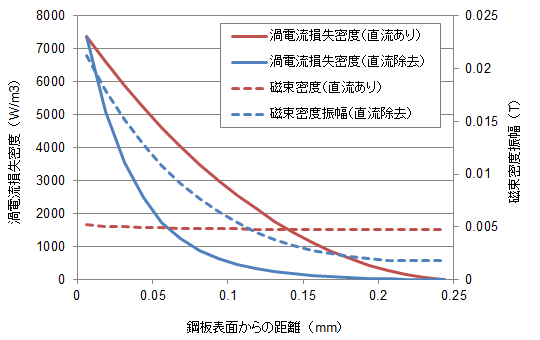図S3.3 ケースDHの鋼板内の磁束密度分布と渦電流損失密度分布直流あり」では磁気飽和により透磁率が下がり表皮効果が緩和されていることがわかる。そのため渦電流損失密度が高くなり、結果損失が高くなることがわかる。
アルゴリズム2では磁束密度の振幅のみを考慮するため直流成分があったとしても「直流除去」の状態として計算を行う。そのためグラフの「直流あり」と「直流除去」の差がアルゴリズム2の誤差となる。
Q4：なぜ直流重畳がある場合、低周波域でのヒステリシス損失が小さいのか？(ケースDL)
ケースDMおよびDHを見るとアルゴリズムによってヒステリシス損失に大きな差が生じています。アルゴリズム2とアルゴリズム3のヒステリシス損失だけ抜き出したものを図S3.4 に示します。
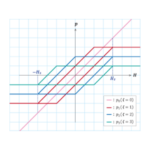
ここまではアルゴリズム間の差は、アルゴリズム3のモデリング能力の高さによって説明されましたが、この差については、アルゴリズム3の問題点の１つを浮かび上がらせています。第9話で述べたとおり、アルゴリズム3ではヒステリシス損失はプレイモデルによって計算されますが、そこで使われるメジャーループ群の磁束密度振幅間隔が、プレイモデルが捉えることができる\(BH\)ループの分解能になっています(図S3.5)。つまり、捉えたい\(BH\)ループの磁束密度振幅が\(\Delta B\)の場合には、メジャーループの振幅間隔は\( 2 \Delta B\)以下にしないといけません。
今回の場合、Q1でも説明した通り、直流重畳によって磁束密度振幅が非常に小さくなっており、0.01T程度になっています。一方、今回使用したメジャーループの振幅間隔は0.05Tで分解能は0.025Tで、0.01Tの振幅をきちんと捉えることができていません。今回のような飽和域でのヒステリシス損失は非常に小さいとはいえ、利用時には注意が必要です。
尚、プレイモデルについては8月に入ってから少し踏み込んだ説明をする予定です。
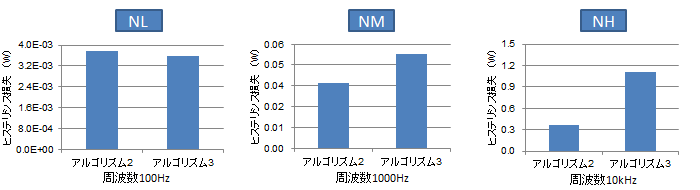(a) 直流成分0A、交流成分振幅 0.01A
(b) 直流成分0.2A、交流成分振幅 0.01A
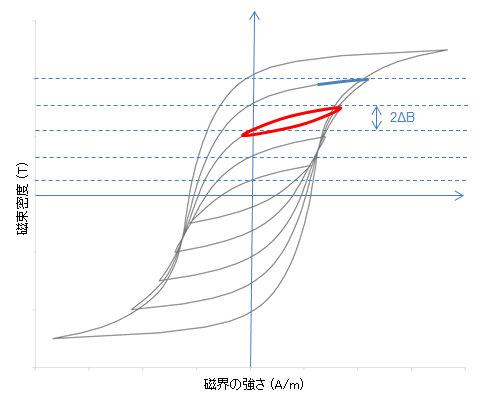図S3.5 メジャーループ群とその分解能メジャーループ群の磁束密度振幅間隔（\( 2 \Delta B\)）がプレイモデルが表現することができる\(BH\)ループの分解能になります。\(\Delta B\)以上の\(B\)の変動幅であれば精度良く扱うことができる。(赤線)れ以下の場合にはループを描くことができない。(青線)
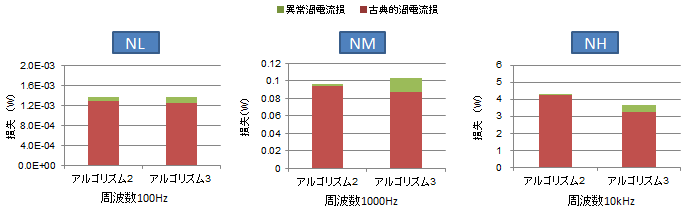
Q5：なぜ直流重畳がない場合、渦電流損失が小さいのか?(ケースNL、NM、NH)
例えばケースNMの場合(図S2.1)、アルゴリズム2の渦電流損失は0.096Wであるのに対し、アルゴリズム3のそれは0.087Wになっており開きがあります。
この差の理由は単純で、アルゴリズム2の計算には異常渦電流損失が含まれているのに対し、第9話でのアルゴリズム3の計算では異常渦電流損失は含まれていなかったためです[*2] 。なぜ、アルゴリズム2では含まれているのに、アルゴリズム3では含まれていないのか、については第12話で述べていますので、頭の中にそのかけらもない人は戻っていただきたいところですが、面倒くさい人のために、今回に限って特別サービスで簡単にまとめましょう。
アルゴリズム2は、測定された鉄損特性をそのまま使います。鉄損特性の測定では、異常渦電流損失を器用に抜き取ることはできず、全ての損失が混然一体となって測定されます。アルゴリズム2では異常渦電流損失は分離によって確認することになります。分離方法については、すみません、これは第12話に戻ってください。一方、アルゴリズム3は、鉄損特性を直接使わずに、ヒステリシス損失と渦電流損失を算出するため、異常渦電流損失は別途計算しないといけません。この計算方法についても第12話に書かれているので、興味のある方はそちらをご覧ください。
では、異常渦電流損失を入れたらどうなるか見てみましょう。全てのケースについてアルゴリズム3については異常渦電流損失を加え、アルゴリズム2については分離した結果を図S3.6 に示します。異常渦電流損失を加えることでアルゴリズム2とアルゴリズム3の結果も差が小さくなることがわかります。
この説明のヘッダを”直流重畳がない場合・・・”としましたが、直流重畳をした場合でも、当然、異常渦電流損失の影響はあります。直流重畳がある場合には、逆にアルゴリズム2とアルゴリズム3の差は広がってしまい、少々不都合な感じもしますが、これはQ3 で説明した通り、アルゴリズム2は渦電流損失を過小評価してしまっているためです。
(a) 直流成分0A、交流成分振幅 0.01A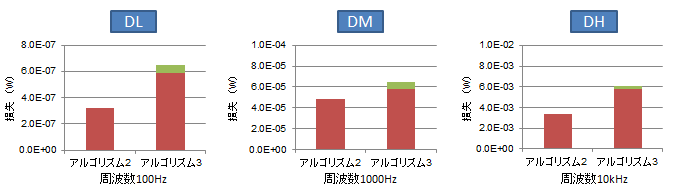
(b) 直流成分0.2A、交流成分振幅 0.01Aアルゴリズム2ではまず渦電流損の総和を計算し、異常渦電流損を分離して求める。アルゴリズム3では異常渦電流損を含まない形で渦電流損を計算し、補正係数から異常渦電流損を求める。特に直流重畳がない場合では渦電流損失の総和はアルゴリズム2と3で近い値を示す。
疑問については一通り説明したつもりですが納得していただけたでしょうか？納得いかん、ということであれば遠慮なく下のコメント欄にご意見をお寄せください。
[*1] ゼロ中心の交流場といっても、直流重畳電流のないケース(NM)とは状況が異なります。ここでの議論は、既に高磁束密度域で発生した1つの磁束密度波形から渦電流を計算する場合に、動作点がどのように影響するかについてです。直流重畳電流の有無は磁束密度波形自体を大きく変えてしまいます。
[*2] 第9話では異常渦電流損失はまだ説明していなかったので計算からも外しました。
