解析屋が見た損失評価
山田 隆
今回は新しい鉄損モデルのお話です。ヒステリシス損失用のプレイヒステロン(以下プレイモデル)と渦電流損失用の均質化法です。それぞれ全く異なるモデルですが、損失発生のメカニズムを内蔵し、従来の鉄損特性データには依存せず、動作域に制限がない点で共通しています。早速始めましょう。
(1)プレイモデル(ヒステリシス損失解析)
プレイモデルは損失モデルではなく、任意のマイナーループを再現する磁化モデルです。損失は磁化の履歴、つまり、BHループの面積から計算することになります。プレイモデルの理論詳細をここで説明すると日が暮れるので、それは他の優れた解説<11><12>に譲るとして、ここでは機能概要について説明したいと思います。理論詳細を知らないんだろう!?って、じょ、冗談じゃありません。そ、そんなことはありません。ほ、本当に時間が・・・
いきなりプレイモデルの説明をする前に、従来の磁化モデルについておさらいをしておきましょう。従来の磁界解析では磁化モデル、つまり、磁化特性を表現するためにはBHカーブが使われています。本当はメジャーループやマイナーループがあって開いた”ループ”になっているのですが、目をぐっとつぶって、ループをぺしゃんこの”線”にしてしまいます(図27)。
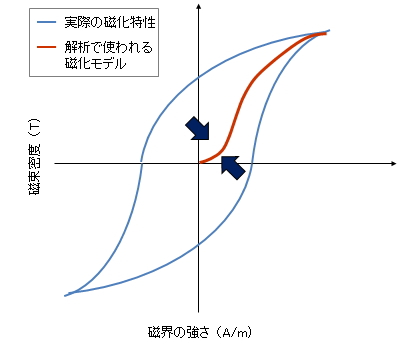 図27 実際の磁化特性と解析で使われる磁化モデル
図27 実際の磁化特性と解析で使われる磁化モデル
これがBHカーブで、通常の解析に使われている磁化モデルです。明らかにこの磁化モデルでは、どのように起磁力が働いても動作点はBHカーブ上を行ったり来たりするだけで軌跡はループにならず、損失も表現できません。そのために、磁界解析の後で測定で得られた鉄損特性をマップする従来法を使うことになります。
一方、プレイモデルは動作点の履歴に応じた任意のマイナーループを再現します。損失はその面積から計算します。魔法のようなプレイモデルですが、もちろん、材料の特性をモデルに埋め込む必要があります。従来の磁化モデルでは、BHカーブ自体が磁化モデルであり、かつ、材料の特性データでもあったわけですが、プレイモデルを特徴付けるためには振幅の異なるメジャーループ群を測定によって準備する必要があります(図28) (*1)。因みに上の例で使ったプレイモデルでは振幅0.5Tから2Tまでの50A470のメジャーループを使っています。
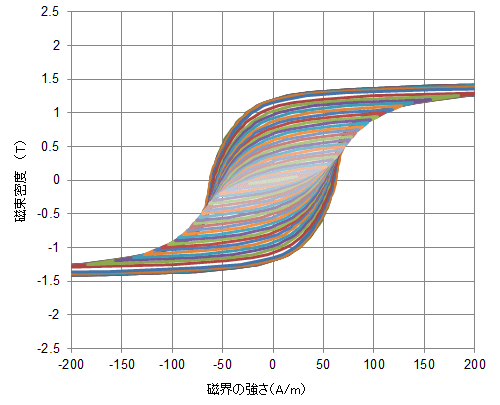 図28 50A470のメジャーループ群
図28 50A470のメジャーループ群磁束密度の振幅を0.05T刻みで0.05Tから2Tまで計40本のループを表示。
同様のデータがJMAGの材料データベースに搭載されている。
実際に見てみましょう。振幅0.2Tの交流に直流を重ねた正弦波波形(磁束密度)かけていきます。その時にプレイモデルから出力されるHの値をプロットしていくと図29のような直流バイアスに応じたマイナーループが得られます。マイナーループの大きさや形がバイアスによって変わっていることがわかります。従来の計算方法、例えば、アルゴリズム2の計算法では、ループの数と振幅は考慮しますが、ループの位置に関わらず同じ値を割り当ててしまいます。この例での比較を図30に示します。
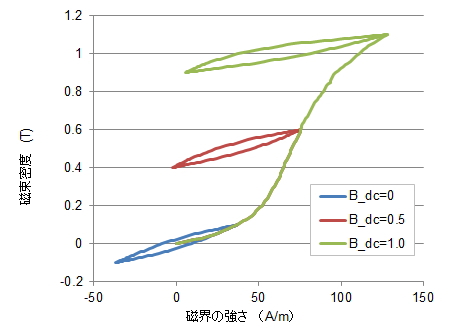 図29 直流バイアスをかけた場合のマイナールループ
図29 直流バイアスをかけた場合のマイナールループ50A470に対して磁束密度の直流バイアスB_dcを0T、0.5T、1T、そのうえに0.1Tの交流成分を重畳させたときのマイナーループを示めす。バイアスが大きくなるに従ってループの面積が大きくなることがわかる。アルゴリズム2では磁束密度の変化量が同じであれば直流バイアスの大きさによらずループの面積は同じとして計算される(鉄損特性の測定状態であるバイアスゼロの値が適用される)。
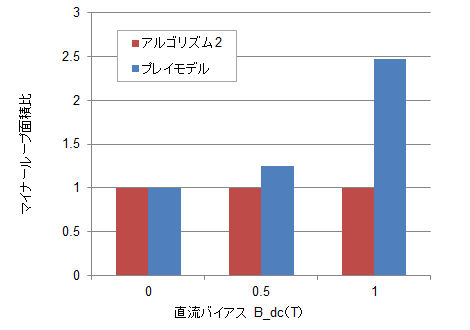 図30 直流バイアスをかけた場合のマイナールループの面積
図30 直流バイアスをかけた場合のマイナールループの面積50A470に対して磁束密度の直流バイアスB_dcを0T、0.5T、1T、そのうえに0.1Tの交流成分を重畳させたときのマイナーループの面積比を示めす。面積比の基準は直流バイアスがゼロの値を1として示した。
アルゴリズム2では直流バイアスによって面積は変わらない(つねに直流バイアスゼロのときの面積が参照されるため)が、プレイモデルではバイアスの大きさによって面積が異なる。
(2)均質化法(渦電流損失)
渦電流損失計算の問題点も、測定に強く依存しているために測定範囲外の周波数では信頼性が保てないことでしたね。渦電流損失のためのモデルも損失発生メカニズムを内蔵する必要があります。ここで紹介する均質化法は、電磁鋼板1枚の中を流れる渦電流を分布を含めて再現し、その渦電流から損失を計算します。したがって、高周波になるにつれ顕著になる表皮効果をきちんと取り込むことができます。特に、電磁鋼板の電気抵抗率1つを与えれば任意の周波数(*2)に対応してくれるところが魅力です。
実際にどのようにそのモデルを実現するかと言えば、損失を評価する全ての要素において、電磁鋼板の厚さ方向に分割を持つ1次元のFEMを行います。これに通常の2次元または3次元の磁界解析によって得られる磁束密度を入力として渦電流密度分布を求めます。
ではこちらも動作を実際に見てみましょう。材料35JN210に振幅0.02Tの正弦波磁束密度を印加し周波数を上げていきます。その時の渦電流損失の変化を図31に従来の解析手法(アルゴリズム1または2)の値とともに示します。
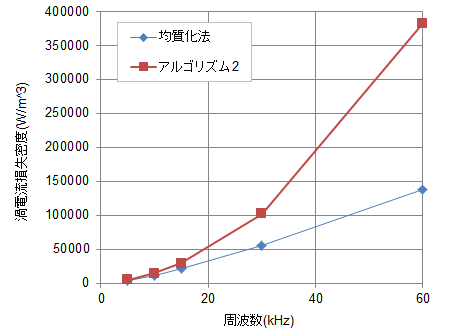 図31 均質化法とアルゴリズム2の渦電流損失の比較
図31 均質化法とアルゴリズム2の渦電流損失の比較35JN210 の単板に対して振幅0.02Tの交流場を印加した際の渦電流損の計算を行った。アルゴリズム2で用いる鉄損特性は10kHzまで存在している。2つの手法は10kHzまでは整合した値となるが、それ以降の周波数では差が大きくなる傾向にある。
周波数が高くなるにつれ従来法と均質化法の差異が大きくなっていることがわかります。これは10kHz以上では測定値がないために周波数の二乗に比例することを仮定して補外したためです。均質化法において表皮効果が考慮されていることを見るために1次元FEMで計算された電磁鋼板内の磁束密度を確認してみましょう(図32)。周波数が上がるにつれて表皮効果によって磁束密度が表面に押しやられている様子がわかります。これによって実効的な抵抗が上昇し渦電流が抑制され周波数の二乗のラインから外れて行きます。
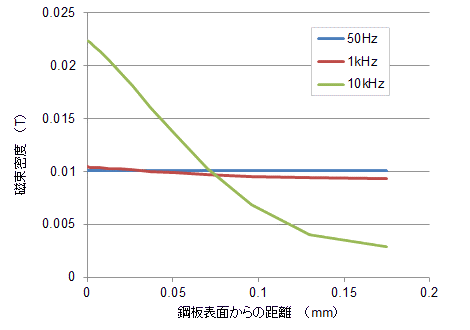 図32 電磁鋼板内の磁束密度分布
図32 電磁鋼板内の磁束密度分布0.35mmの鋼板に振幅0.02T、周波数を50Hz, 1kHz, 10kHzの磁束密度を印加した場合の鋼板内の磁束密度分布。 50Hz, 1kHzに比べて10kHzでは表皮効果の影響を見ることができる。
さて、これでヒステリシス損失と渦電流損失に対する新しい鉄損モデルが揃いました。この鉄損モデルのアルゴリズムにも名前を付けましょう。はい、”アルゴリズム3″です。アルゴリズムの数が増えてきたのでここで一度整理しておきましょう。表3に手法と特徴をまとめておきます。
| アルゴリズム1 | アルゴリズム2 | アルゴリズム3 | ||
|---|---|---|---|---|
| ヒステリシス 損失 |
手法 |
|
|
プレイヒステロンモデルによって計算された任意マイナーループの面積から計算 |
| データ | 鉄損特性データ | 鉄損特性データ | メジャーループ群 | |
| 誤差要因 | ・正弦波から歪んだ磁束密度 ・直流バイアスの磁束密度 |
直流バイアスの磁束密度 | ||
| JMAGの 設定 |
FFT | ループを考慮 | ヒステリシスモデル | |
| 渦電流損失 | 手法 | 鉄損からヒステリシス損を差し引いて計算 | 鉄損からアルゴリズム1の方法で計算されたヒステリシス損を差し引いて計算 | 均質化法による渦電流分布から計算 |
| データ | 鉄損特性データ | 鉄損特性データ | 電気抵抗率 | |
| 誤差要因 | 特性データの範囲外の周波数帯での計算 | 特性データの範囲外の周波数帯での計算 | 異常渦電流損 | |
| JMAGの 設定 |
FFT 設定方法の動画はこちら (第3話 図8) |
FFT 設定方法の動画はこちら (第4話 図15) |
積層解析 設定方法の動画はこちら (第9話 図33、34) |
|
また、JMAGでの設定方法についてもここで説明しておきましょう。鉄損条件の設定においてヒステリシス損をヒステリシスモデルに、ジュール損を積層解析とします(図33)。材料特性の設定もこれまでと変わりますので注意してください。プレイモデルのためのメジャーループの設定は鉄損タブで行います。メジャーループはJMAGに搭載されているものも使えますし、自分で入力したい場合には材料パネルの新規作成ボタンから行えます(図34)。均質化法のための電気抵抗率の設定は従来通り材料パネルの電気特性タブで設定した値が使われます。
図33 アルゴリズム3による損失計算の設定方法
図34 アルゴリズム3に必要な材料特性の設定
ではアルゴリズム3を使って鉄損を計算してみましょう。計算対象は第4話で使ったリングコアです。コアの材質は50A470です。コイルに正弦波電流を流し、さらにそこに直流電流を加えます(図35)。この正弦波電流の周波数と直流電流を変えた場合の鉄損を計算してみました(図36)。比較のためにアルゴリズム1および2の結果も載せておきます。結果を見ると、アルゴリズム間で同じであったり違ったりしていますが、その理由は何でしょうか。これは練習問題にしておきましょう。
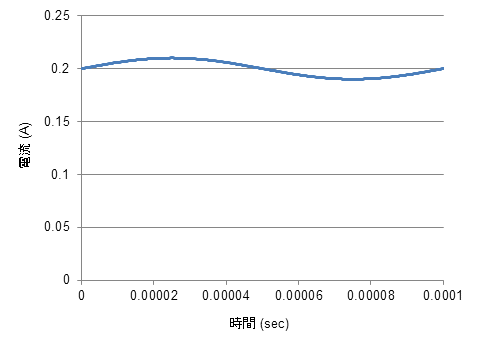 図35 直流重畳電流波形
図35 直流重畳電流波形直流成分 0.2Aに対して振幅0.01A、周波数10kHzの交流成分を重畳したものを印加。
電流振幅の大きさは磁束密度の振幅がおよそ0.2Tになるように決められた。
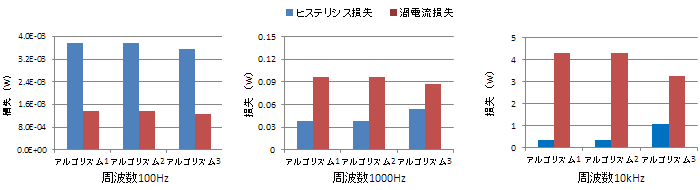 (a) 直流成分0A、交流成分振幅0.01A
(a) 直流成分0A、交流成分振幅0.01A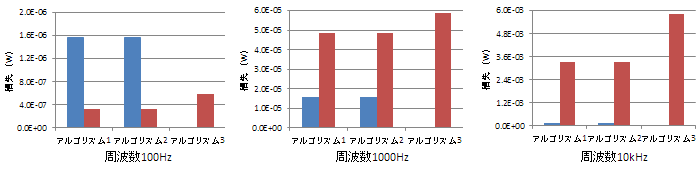 (b) 直流成分0.2A、交流成分振幅0.01A
(b) 直流成分0.2A、交流成分振幅0.01A50A470に直流成分が重畳した正弦波電流を印加してアルゴリズム1,2,3の結果を比較。
直流電流の大きさ、交流成分の周波数を変えて計算を行った。
トロイダルコアに対して正弦波の電流を投入しているので必ずしも磁束密度は正弦波状にはならない、また直流成分によるマイナーループの影響、高周波による表皮効果がどう各損失に影響するかを考慮にいれながら結果を評価する必要がある。
次回はこの新しい鉄損モデルを使ってモータの鉄損を計算してみます。
[*1] 隣合うメジャーループの振幅間隔が再現できるマイナーループの振幅を決定しますので、小さなマイナーループを見ようと思えば間隔を密にする必要があります。
[*2] ただし、後述するように電磁鋼板を有限な厚さで分割するため、現実的にはその厚さが扱える周波数の上限になります。