解析屋が見た損失評価
山田 隆
さて、まず、鉄損についてです。
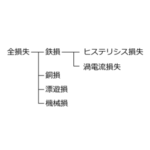
今も昔も解析ニーズは高く、最初に機能リクエストを受けたのも鉄損でした。第1話の分類のとおり鉄損は3つに分類できるのですが、まずは鉄損の計算方法を見てみたいと思います。
「それぞれについて見なくても良いのか?」ですか。
はい、良いと思います。そんなことを知らなくても鉄損は計算できてしまいます。まあ、こういう態度が過ぎて大きなシッペ返しを受けるのですが、その話は後程。
モータやトランスなどの電気機器は百年を超える歴史を持っており、昔も今も世の中で最優秀なエンジニアがその改良に取り組んできています。その先人たちの技術とノウハウの蓄積はまさに文明です。その文明の中に、鉄損評価というものがあり、コアに使われる電磁鋼鈑は、ほとんどの場合、鉄損の特性データが利用可能になっています。鉄損特性の一例を図2に示します。横軸が磁束密度、縦軸が鉄損密度で、周波数毎の曲線で与えられます。曲線のことを鉄損曲線と呼びます。
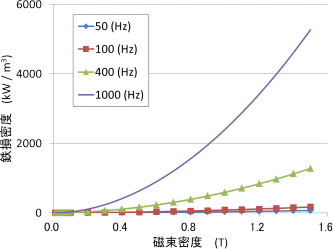 図2 電磁鋼板(50A1300)の鉄損特性
図2 電磁鋼板(50A1300)の鉄損特性
一方、コアの磁束密度の空間分布と時間変動は磁界解析をすれば求めることができます。ただ、モータの場合、時間変動はほとんどの場所で正弦波ではなく、たくさんの周波数成分を含んだ複雑な波形をしていますので、周波数に分解する必要があります。例として、図3にある正弦波駆動のモータのティース中央における磁束密度の時間変動とそれを周波数に分解したグラフを示します。周波数への分解を数式でも書いておきましょう。
\( B(t,x) = \displaystyle \sum_{l}B_l(x)e^{j\omega lt} \quad \cdots \) (1)
\( B(t,x) \):時刻\(t\), 場所\(x\)における磁束密度(T)
\( B_l(x)\):第\(l\)次成分の場所場所\(x\)における磁束密度(T)
\( \omega_l \):第\(l\)次の角度周波数
実際の計算ではすべての要素についてこの分解を行います。つまり、1万要素ある場合には1万個のデータを作ることになります。大変な量ですが、心配ご無用、やるのはJMAGとコンピュータです。
さて、これで要素毎に、周波数毎の磁束密度を持つことができたわけですから、先の鉄損特性データを使えば要素毎の損失密度を求めることができます。その後、要素の体積をかければ要素毎の損失が求まり、これをステータ、ロータ毎に足し合わせれば、部品毎の損失量を得ることができます。これも数式でまとめておきましょう。
\( P_{tot} = \displaystyle \sum_{k} \sum_{i}p(f_i,B(k,i))a_k \quad \cdots \) (2)
\( P_{tot} \):注目する領域の損失総量
\( k \):注目している領域に属する要素番号
\( f_i \):第第\( i \)次次の周波数(Hz)
\( B(k,i) \):第\( k \)要素の第\( i \)次成分の磁束密度
\( p(f,B) \):周波数\( f \)、磁束密度\( B \)における損失密度
\( a_k \):第\( k \)要素の体積
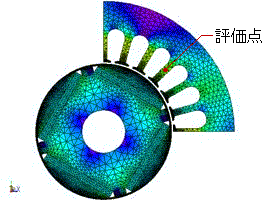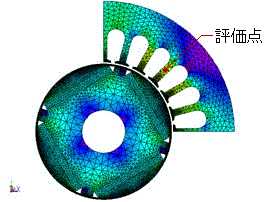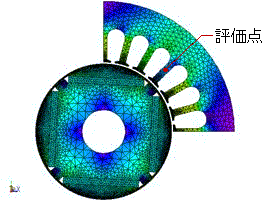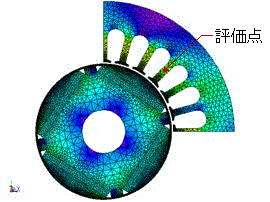 (a) モータの磁束密度コンターと評価点
(a) モータの磁束密度コンターと評価点
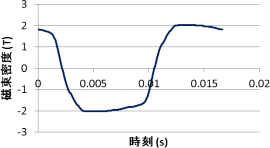 (b) 評価点における磁束密度の時間変化
(b) 評価点における磁束密度の時間変化
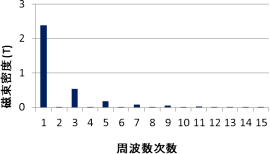 (c) 磁束密度の周波数分布
(c) 磁束密度の周波数分布
正弦波駆動にもかかわらず、諸々の影響によって波形は単純な正弦波ではなく、複数の周波数成分を持っている。
計算は少々ややこしくなりましたが、通常の磁界解析と鉄損特性データを使うことで鉄損を計算することができました。いろいろと気になる点がないわけではありませんが、それは追々考えることにいたしましょう。また、いつでもここに戻ってこられるように上で述べた計算手順(アルゴリズム)に”アルゴリズム1″と名前を付けておきましょう。
次回は、損失の分離について考えます。