解析屋が見た損失評価
山田 隆
今回はアルゴリズム3を使ったモータの鉄損計算を見てみたいと思います。
最初はSRモータです。モータの外観および仕様はそれぞれ図37と表4の通りです。また、それぞれの鉄損計算で使った材料特性データを表5と図38にまとめておきます。
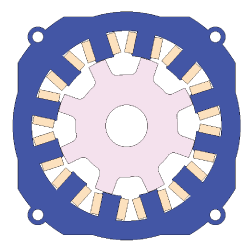 図37 SRモータのモデル
図37 SRモータのモデル
| ステータ外径 (mm) | 136 |
| ロータ外径 (mm) | 83 |
| ギャップ長 (mm) | 0.3 |
| 積厚 (mm) | 70 |
| 相数 | 3 |
| 突極数 | 12/8 |
| 鋼板材料 | 50A1300 |
| 巻数/相 | 120 |
| 相抵抗 (室温)(Ohm) | 0.44 |
| アルゴリズム2 | アルゴリズム3 | |
|---|---|---|
| ヒステリシス損失 | 鉄損特性データ [*1] | メジャーループ群(図38) |
| 渦電流損失 | 鉄損特性データ [*1] | 電気抵抗率:1.4e-07(Ohm/m) |
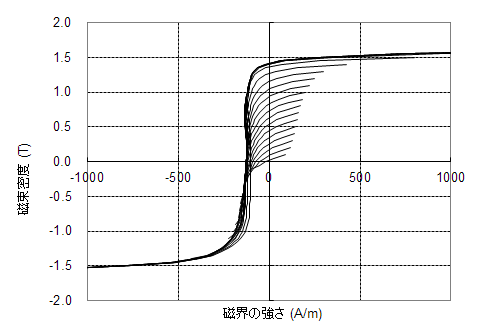 図38 50A1300の対称ループ (アルゴリズム3で使用)
図38 50A1300の対称ループ (アルゴリズム3で使用)
アルゴリズム3による鉄損計算の結果を実機測定の結果とともに図39に示します。比較のためにアルゴリズム2による結果も載せておきます。
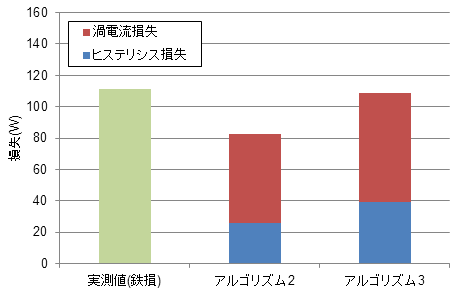 図39 実測と解析の比較
図39 実測と解析の比較回転数3,000(r/min)において鉄損の実測値に対してアルゴリズム3の結果がよく一致していることが分かる。
一方でアルゴリズム2は過小評価する結果となっている。
この結果を見ると、アルゴリズム3は実機の損失を良く再現していることがわかります。一方、アルゴリズム2の結果は今一つです。第7話では我らが晴海1号の損失をアルゴリズム2が良く再現していたことを見ました。なぜ、このSRモータではダメなのでしょうか?その謎を解く鍵は駆動電流にあります。図40に駆動電流波形を示します。
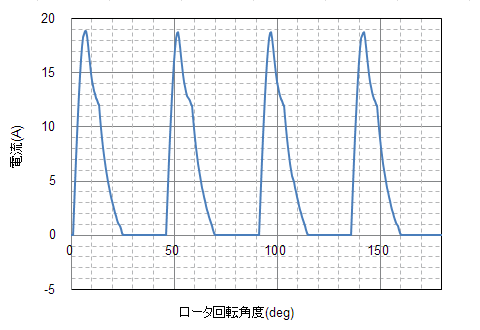 図40 駆動電流波形
図40 駆動電流波形
SRモータでは晴海1号のような交番電流ではなく、正方向だけに電流が流れる半波波形をしています。このような片側に偏った電流波形が作る磁束密度波形はマイナーループを作りそうです。実際、モータ内部のいくつかの点におけるBHの軌跡を描いてみると図41のようなゼロを中心としないマイナーループになっていることがわかります。
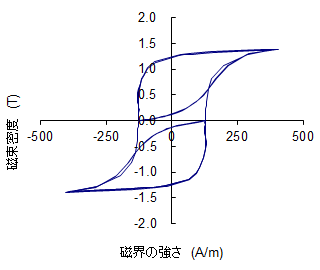 (a) ロータ部歯先(図(c)中の点A)
(a) ロータ部歯先(図(c)中の点A)
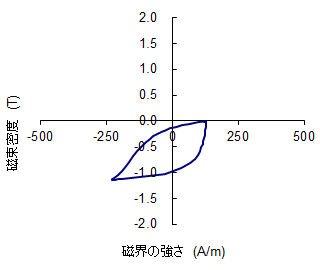 (b) ステータ部ティース先端(図(c)中の点B)
(b) ステータ部ティース先端(図(c)中の点B)
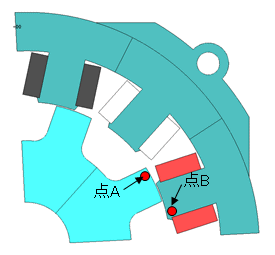 (c) SRモータモデルと測定点
(c) SRモータモデルと測定点図41 モータ各部におけるBHの軌跡
回転数1,000(r/min)時の、SRモータの(a)ロータ部歯先(図(c)中の点A)と(b)ステータ部ティース先端(図(c)中の点B)におけるBHの軌跡を示す。両者ともに原点を中心としないマイナーループとなっている。
このようなマイナーループはアルゴリズム2にとって苦手な相手でした。ヒステリシス損失の計算の精度に不安を覚えます。逆に、アルゴリズム3にとってはマイナーループなど朝飯前です。
渦電流損失に関しては、アルゴリズム間で大きな差は出ていません。これは、このケースでは、回転数がそれほど高くなく、高調波成分も大きくないために、従来の方法でも十分に対応できたためです。念のために各点の磁束密度波形の調波分析を図42に示します。高次成分はあるものの鉄損特性の測定周波数~10(kHz)に収まっていることが確認できます。
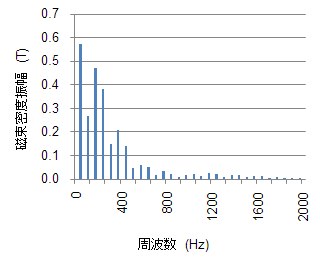 (a) ロータ部歯先
(a) ロータ部歯先
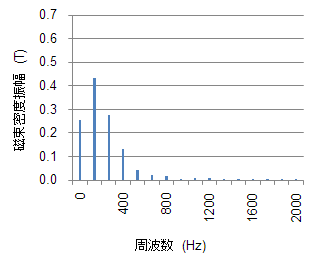 (b) ステータ部ティース先端
(b) ステータ部ティース先端
図41に示した各部のBH軌跡に対する調波分析結果をそれぞれ(a)ロータ部歯先、(b)ステータ部ティース先端に示す。高次成分はあるものの有意な成分は鉄損特性の測定範囲である10kHz以下に収まっていることが分かる。
次に再び晴海1号(IPM)での結果です。モータの仕様、駆動条件などは第7話表2をご確認ください。上と同様にアルゴリズム3による結果を実測値およびアルゴリズム2の結果とともに図43に示します。
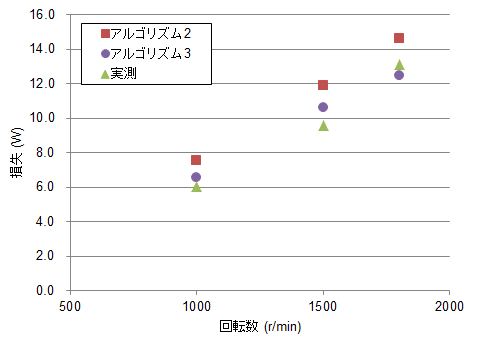 図43 実測と解析の比較。
図43 実測と解析の比較。回転数1,000(r/min)から1,800(r/min)のそれぞれにおける、晴海1号(IPMモータ)鉄損を実測とアルゴリズム3で比較する。
アルゴリズム2の結果(第8話の図23)と比較して改善されていることが分かる。
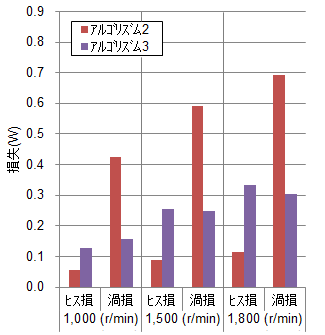
今回は大サービスで解析で得られた損失をステータコア、ロータコア、磁石に分けたうえで、それぞれをヒステリシス損失、渦電流損失に分離した結果も載せましょう(図44)。
このように損失を細かく分離できることは解析の大きなメリットです。
第7話で示した通り、アルゴリズム2でも良い結果が出ていましたので、アルゴリズム3によって大きな変化は望めない、というか、望まないのですが、それでも若干改善され測定値に近づいていることが図43からわかります。
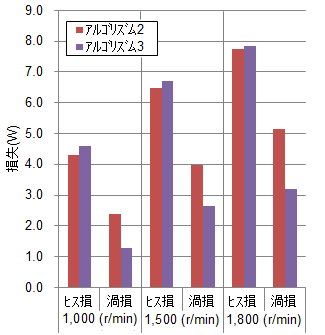 (a) ステータコア
(a) ステータコア
 (b) ロータコア
(b) ロータコア
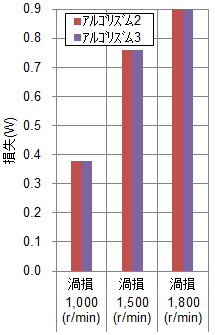 (c) 磁石
(c) 磁石
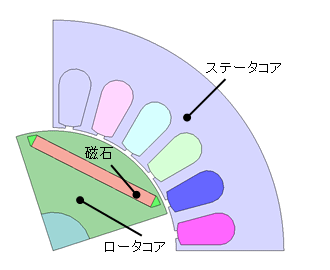 (d) IPMモータと部品名称
(d) IPMモータと部品名称
図43に示したようにアルゴリズム3を使用することでより実測近づく結果が得られた。その要因としてステータコアに発生する渦電流損失の寄与が大きいことが分かる。
アルゴリズム3で精度が改善された理由を考えるために図44を見てみると、ステータの渦電流損失がアルゴリズム2の結果に比べてアルゴリズム3のそれは小さくなっていることがわかります。これは第8話(課題2)でも触れたとおり、アルゴリズム2では鉄損特性の測定範囲外は周波数の二乗に比例するとして第8話図24補外してしまうため、一般に、過大評価をしてしまうためです。第8話図24で示したティース中央部の磁束密度波形の調波分析(図45)を見てみると、今回使った鉄損特性の上限である10kHzを超えて、高周波成分が存在しています。参考のために1800(r/min)での渦電流損失の周波数分解を図46に載せます。図45と比べると磁束密度では小さい高周波成分も損失になると大きな寄与をしていることがわかります。これは、微小な磁束密度も精度良く計算しないと損失に大きな誤差を与えてしまう可能性を示唆しています。
アルゴリズム3では、そのような高周波域になっても均質化法が対応してくれるので安心です。今回のケースでは回転数が高くないのでその違いは顕著ではありませんが高回転域で使う場合には渦電流損失の扱いは重要なポイントになってきます。
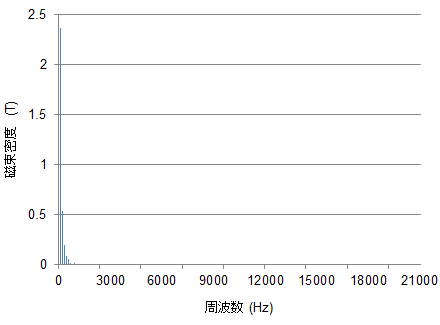 図45 ティース中央部における磁束密度波形の調波分析
図45 ティース中央部における磁束密度波形の調波分析第8話の図24に示したティース中央部における磁束密度波形に対する調波分析結果を示す。
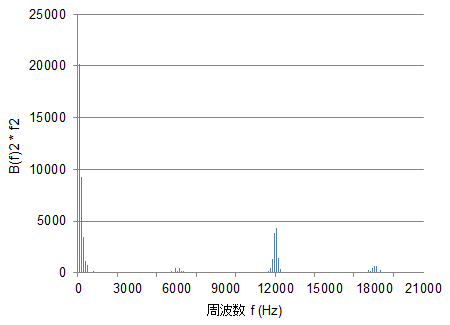 図46 渦電流損失の調波分析
図46 渦電流損失の調波分析渦電流損失に対する調波分析結果を示す。縦軸は渦電流損失の大きさの指標として図44で示した周波数ごとの磁束密度の2乗に周波数の二乗をかけたものを示した。
渦電流損失は周波数の二乗で効くため、磁束密度では小さい高周波成分も渦電流損失では大きな成分になることが分かる。
もう1つ重要なポイントを見ておきたいと思います。図44(b)のロータコアのヒステリシス損失を見てください。それ自体、損失全体から見れば目立たないのですが、アルゴリズム間で大きな違いがあることがわかります。その原因を探るためにロータ表面付近のコアの磁束密度波形を見てみましょう。これは第8話の図25でも見ましたね。そこでもコメントしたのですが、ロータ上では磁石磁束が直流分としてバイアスされるために動作点がマイナーループを形成します(図47)。
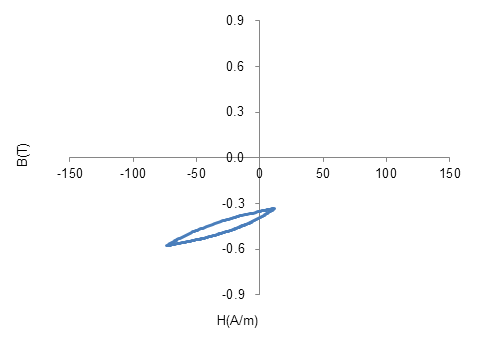 図47 ロータ表面部におけるBH軌跡
図47 ロータ表面部におけるBH軌跡ロータ表面部におけるBHの軌跡を示す。磁石磁束の影響で直流成分がバイアスされた状態でマイナーループを描いていることが分かる。
これはアルゴリズム2にとっては苦手、アルゴリズム3には得意な状況です。ロータの損失を気にする人は注意しないといけません。
いかがでしょうか。新しい鉄損モデルを使ったアルゴリズム3のメリットを感じていただけたでしょうか。アルゴリズム3はこれまでと異なりメジャーループ群が必要になりますが、従来の方法が抱えていた問題を根本から解決し、精度と適用範囲を大幅に改善しています。ぜひ、挑戦していただきたいと思います。
鉄損についてはお話ししたいこと、恐らく、しなくてはならないことがまだまだあるのですが、ここで一旦鉄損から離れ、こちらも重要性ではひけをとらない漂遊負荷損に目を転じたいと思います。明日はそのお話です。
[*1] 第2話図2参照