解析屋が見た損失評価
山田 隆
このコラムも終わりが近づいてきました。残された話題は技術的に未解決のものばかりです。気は重くとも損失は発生しています。勇気を振り絞って課題についてまとめたいと思います。
<応力依存性>
圧縮応力によって磁化特性が大きく劣化することなどは材料研究の分野ではよく知られており、モータのステータの焼嵌めの影響については多くの議論がされてきました<34>。
この応力依存性の問題には二つの技術的な課題があります。1つは材料特性の測定です。モータの中では100MPa近い応力が発生している可能性がありますが<35>、測定ではそのような高い応力状態で安定的に材料特性を測定することは現時点では難しいようです。ただ、測定方法の改良も進められており近い将来、十分な範囲をカバーできるようになると期待されています<36>。
もう一つの課題は、異方性に関してです。磁化特性は圧縮方向と引張り方向では著しく異なります<37>。一般にある方向に圧縮されている場合には、その直角方向は引張り状態になっているため(図54)、磁化特性として異方性になります。また、場所ごとに応力状態が異なるため異方性の扱いも単純ではありません。そのため非線形反復計算の収束性が悪化するなども難しさもあります。
難しさがあるにせよ、損失に影響を与えるのであれば取り組まないわけにはいきません。幸いなことにモータの場合にはギャップがあるため、多くの場合、特に永久磁石モータの場合には、磁化特性についてそれ程神経質になる必要はなく、損失への影響に注目すればよさそうです。この考え方<38>で実測を良く再現する解析が行われています。また、この解析では損失特性の実測値が十分に得られないため、入手可能なデータから関数形を推定して応力による特性変化を考慮しています。必要なことは知恵を絞ってやる、という迫力を感じさせる論文です。
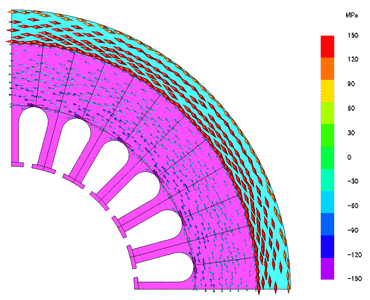図54 焼き嵌めによるステータコアの応力分布焼き嵌めにより外側のフレームには引っ張り応力が発生し、ステータコア、とくにティース根元には圧縮応力が生じる。
JMAGの鉄損解析ツールでも応力分布を取り込んだ解析が可能です(図55)。応力分布はJMAGの構造解析を使っても良いですし、Abaqusなど他の構造解析ツールの結果を使うこともできます。応力依存特性の指定はテーブルで行います。解析例はJMAGのアプリケーションノート 87「焼き嵌めを考慮したIPMモータの鉄損解析」にありますのでご覧ください。
図55 応力分布を取り込んだ鉄損計算の設定方法
<加工歪>
打ち抜きなどの加工歪による磁化特性の劣化、損失の増大はかなり以前から指摘されており、材料の分野では研究も進められています<39>-<41>。一方、解析の分野では例も少なく標準的なアプローチもまだ定まっていません<42>-<46>。解析計算としては劣化した部分の特性を劣化後の特性に置き換えるだけなので、大きな難しさはありませんが、厄介なのはその劣化特性の取得です。劣化特性は切断面から内部に向かって応力状態とともに変わりますが、その変化は複雑な上、幅全域に渡って測定することはできません。ある程度の推測が必要です。また、加工歪の場合、加工の方法によって劣化特性が変わるため、もはやそれは材料固有の性質ではないことです。したがって、材料メーカが提供できる情報ではなく、加工を行っているユーザ側が測定せざるを得ないのではないかと思います。
一方で打ち抜きは製造上不可避ですので何とかしなくてはなりません。JMAGとしてもここで頑張ってみたいと思います。少ないながらも先行事例はありますので、それを辿ってみることにしました。事例はそれぞれ工夫が凝らされていますが、複数の幅を持つ試料の測定から劣化特性を推定するという考え方は共通です(図56)。現時点ではまだ上手くいっているわけではないのですが、何をやってきたかだけでもお伝えしたいと思います。
まず、方針を説明しましょう。ここでは切断による電磁鋼鈑の特性(磁化特性または鉄損特性)の劣化を劣化量というもので表現します。劣化量は切断面で最大で内部に行くに従って緩和されると仮定します(図57)。また、この関数形を切断幅の異なる複数の試料の測定によって同定することが目的になります。ここでは、関数形は切断幅には依存しないことを仮定します。
測定の仕様を表8にまとめます。
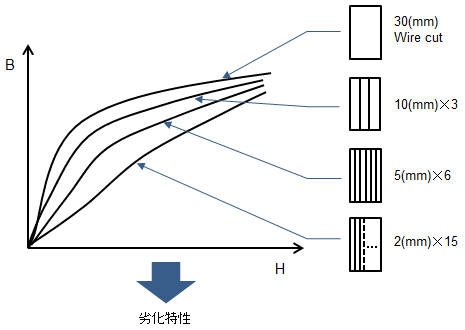図56 劣化特性の推定プロセスワイヤーカットの単板を基準に複数の切断幅の単板を用意。例えばワイヤーカット30mmを用意した場合、10mmに切断した単板を3枚合わせて測定する。目的は各切断幅の磁化特性・鉄損特性に整合した劣化特性を求めること。
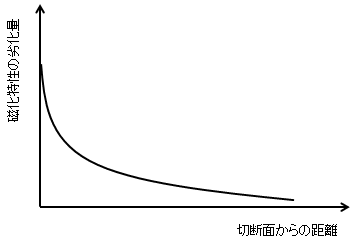図57 切断からの距離と磁化特性の劣化量鋼板を打ち抜いた場合、劣化が最も大きいのは切断面付近であり、距離が離れるに従い劣化量は小さくなる。
| 磁化特性測定装置 | 岩通B-HアナライザSY-8219 | |
| 測定項目 | 直流磁化特性 鉄損特性 |
|
| 直流磁化特性 | ～1.7 (T) | |
| 鉄損 | 磁束密度 (T) | 0.4, 0.6, 0.8, 1 |
| 周波数 (Hz) | 50，100，200，400，100 | |
| 測定単板幅 (mm) | 30 | |
| 単板切断幅 (mm) | 1, 2, 5, 10 [*1] | |
| 切断方法 | シャー切断(劣化あり) 30mmはワイヤーカット(劣化なし) |
|
試料はシャー切断によって切り出しています。実際には打ち抜きで、その違いも懸念されるのですが、シャー切断による事例もありましたので、今回はそれを採用しました。シャー切断によれば、打ち抜きの型を準備せずに、任意の幅の試料が準備できるメリットがあります。もちろん、特性が大きく変わるようでは元も子もありませんが、やってみないとわかりません。これを進めて結果を見たいと思います。
切り出された試料を、参照試料(ワイヤーカット)と同じ幅(今回は30㎜)になるように並べ、これの磁化特性を測定します。測定装置も市販の装置を使っています。尚、測定は今回も芝浦工業大学の赤津先生の研究室にご協力をいただきました。切断幅2mm場合の様子を図58に示します。幅が狭くなるにつれて設定も測定も難しくなってきます。
測定の結果得られた磁化特性と鉄損特性を図59に示します。間違いなく、切断によって特性が劣化しています。しかし、現在のところ、これらの結果を全て満足するような関数形が同定できていません。測定のバラつきによるものか、設定した仮定が適切ではないのか、検討が必要です。
図58 単板2mmの測定の様子2mm幅の単板を15枚合わせて30mmとして測定。
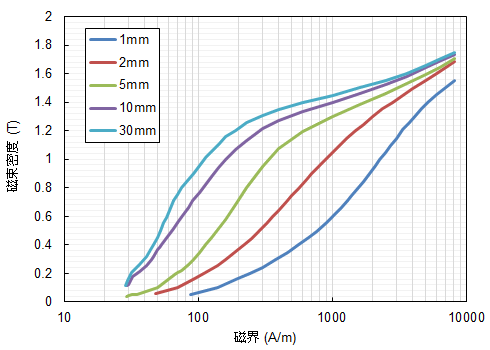(a)磁化特性
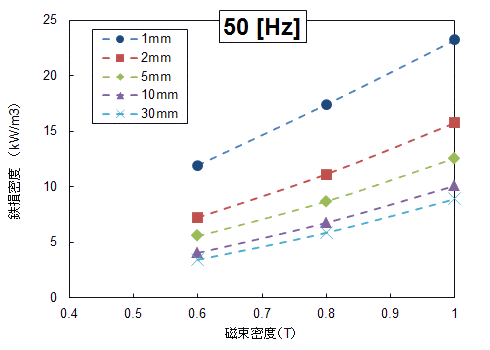(b)鉄損特性単板を1～10mmに切断したものと30mmのワイヤーカットの特性を表示。鉄損特性については50Hzのものを表示。単板の幅が狭くなるほど、磁化特性の劣化および鉄損の増加の傾向が見られる。磁化特性については高磁界より低磁界域で磁化特性の劣化が見られる。
残念ながら私たちのところでは合理的な劣化特性が得られていませんが、文献のように成功しているグループもあるようですし、これを読んで取り組むグループも出てくるかもしれません。私たちは材料特性の取得と並行して、それを使うための機能をJMAGに組み込みました。劣化の影響を考慮したい切断面と深さを指定すると、劣化特性を反映させるための層状のメッシュが自動的に生成され(図60)、別途指定する関数に応じた劣化特性が層毎に設定されます。例として晴海1号に表9のような指定をして損失計算をした結果を図61に示します。
加工歪についてはまだ検討が始まったばかりです。私たちの試みについては逐次お伝えしていきたいと思います。皆さんからのご意見などもお寄せいただければと思います。
加工歪条件にて歪の幅と、層数を入力すると自動メッシュ生成後に層状のメッシュが生成される。解析時に各層の領域には条件を指定したエッジ・面からの距離に応じて劣化した磁化特性・鉄損特性が適用される。
| 回転数 (r/min) | 1000 |
| 電流振幅(A) | 5 |
| 電流位相(deg) | 0 |
| 加工歪条件 | ステータコア、ロータコアに設定 歪幅 2mm / 層数 2 |
| 鉄損条件 | ヒステリシス損：ループを考慮 ジュール損：FFT |
| ロータコア、ステータコア | 35A210 崩壊定数(磁化特性) 200 崩壊定数(鉄損特性) 500 |
ロータコア、ステータコアの劣化係数は5mm幅の単板測定値から同定
崩壊係数は磁化特性の透磁率劣化率と鉄損特性のヒステリシス損増加率の空間分布関数を表すexp関数の係数を表す。
崩壊係数200とは1000mmに対して200mmで減衰することを意味する。
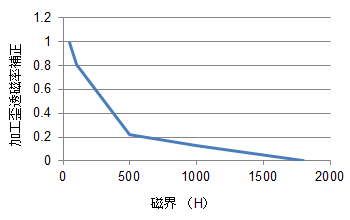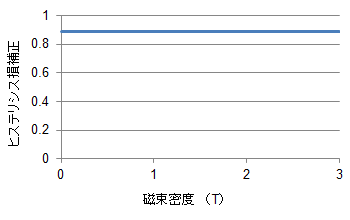
(a) 加工歪透磁率補正切断面における透磁率の劣化率の点列。
低磁界では1に近い値をしめしており、これは透磁率の劣化が大きいことを意味している。上記データは5mm幅の単板から同定
(b) ヒステリシス損補正切断面におけるヒステリシス損の増加量の点列。材料がもつヒステリシス損に対して補正をかけた量が上乗せされる形となる。
(c)ヒステリシス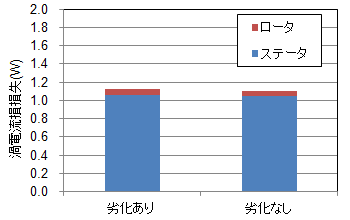損
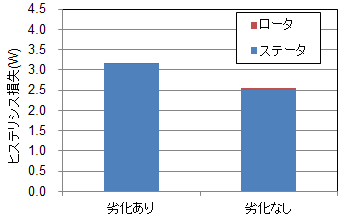
(d)渦電流損加工歪により(d)に示した渦電流損はほとんど影響を受けないが、(c)に示したヒステリシス損はステータで25％増加している。
＜異常渦電流損失＞
最後の最後に異常渦電流損失が残ってしまいました。これも解析としては非常に扱いにくい相手なのでできれば相手にしたくないのですが、損失として存在する以上無視するわけにはいきません。
異常渦電流損失は鉄損の一つに分類され、周波数依存性を持つことから渦電流損失の一部とみなされることもあります。今まで述べてきた渦電流損失は、１枚の電磁鋼鈑を１つの導体の塊としてその中を還流する渦電流による損失ですが、異常渦電流は、磁壁の移動に伴って発生する渦電流とされています<47>。通常の渦電流損失を異常渦電流損失と区別するために古典的渦電流損失と呼ぶこともあります。ここでもそれを使いたいと思います。
異常渦電流損失は、発生メカニズムが複雑であり、材料の個体間のバラつきもあるため、解析での一般的な扱いが非常に難しい損失です。実は不思議なことに、そして困ったことに、定量的な定義も複数あります。ただ、基本的な考え方は共通していると私は思うので、そこから説明したいと思います。
基本的な考え方は非常にシンプルです。異常渦電流損失\(P_{ex}\)は全鉄損\(P_{tot}\)から、ヒステリシス損失\(P_h\)と古典的渦電流損失\(P_{ec}\)を差し引いた残り、と一般に定義されます。式で書くと次のようになります。
\(P_{tot} = P_h + P_{ec} + P_{ex} \quad \cdots \) (12)
おお、簡単ではないか感嘆してはいけません(すみません、完全にオヤジギャグ入りました、少々疲れています。気が付かなかった人は気にしないでください。)。第3話で古典的渦電流損失は全鉄損からヒステリシス損を引いたものだ、としてしまったので、実はその渦電流損失には異常渦電流損失も含まれていることになります。つまり、
\(P_{tot} – P_h = P_{ec} + P_{ex} \quad \cdots \) (13)
そうすると、異常渦電流損失を抽出するためには、その全渦電流損失\((P_{ec} + P_{ex})\)から古典的渦電流損失を引かなくてはなりません。では、その古典的渦電流損失とは何でしょうか？これは一般に、表皮効果を無視した古典的渦電流損失になります。表皮効果を無視した場合、古典的渦電流損失は次のように電磁鋼鈑の厚さ\(d\)と抵抗率\(p\)、磁束密度\(B\)、周波数\(f\)で書くことができます<48>。
\( P^n_e = \large \frac{\sigma(\pi fdB)^2}{6p} \quad \cdots \) (14)
これで、めでたく異常渦電流損を決めることができました。
\( \begin{eqnarray} P_{ex} &=& P_{tot} – P_h – P^n_e \\ &=& P_{tot} – P_h – \frac{\sigma(\pi fdB)^2}{6p} \end{eqnarray}\quad \cdots \) (15)
上で定義が複数あると書きましたが、それは、周波数が高くなっていったときの考え方に違いがあるからです。ここは本当にバラエティに富んでいるようなのですが、比較的よく用いられているものを3つ紹介します。
<異常渦電流損の定義(1)>
(15)をそのまま使います。
<異常渦電流損の定義(2)>
利用可能なもっとも周波数の低いデータを使って、(14)によって低周波\(f_{low}\)の異常渦電流損失\(P_{ex}(f_{low})\)を求め、それ以上の周波数では周波数の1.5乗に比例するとします。式で書くと次のようになります。
\(P_{ec}(f) = P_{ex}(f_{low}) \times (\frac{f}{F_{low}})^{1.5} \quad \cdots \) (16)
その後、測定値(\(P_{tot}\))との整合性をとるために、古典的渦電流損失を次のように求めます。
\(P_{ec}(f) = P_{tot} – P_h – P_{ex}(f) \quad \cdots \) (17)
<異常渦電流損の定義(3)>
鉄損の周波数依存性を次のように仮定し、測定値から係数\(K_h\)、\(K_e\)、\(K_{ex}\)を同定します。
\(P_{tot} = K_h \times f + K_e \times f^2 + K_{ex} \times f^{1.5} \quad \cdots \) (18)
上式によって周波数全域の各鉄損を求めます。
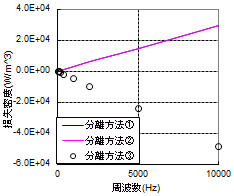
上に紹介した方法は、それぞれに優劣がある上に歴史的な背景もあり、どれが一番とは決められません。一例に過ぎませんが、典型的な材料についてそれぞれの方法で分離した結果を図62に示します。中には損失が負になってしまうものもあり、一筋縄ではいかないことがわかると思います。
(a) ヒステリシス損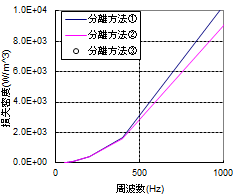
(b) 古典的渦電流損
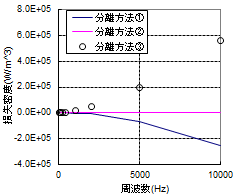(c) 異常渦電流損異常渦電流損の定義①～③に従って35H470の鉄損特性を分離した結果。
方法によってはヒステリシス損や異常渦電流損が負の値になってしまうことがある。①や③では古典的渦電流損に表皮効果が含まれていないため、古典的渦電流損の値によっては異常渦電流損が負になる場合がある。
ところでJMAGではどうしているか、気になりますよね。はい、JMAGのアルゴリズム1と2では上の異常渦電流損の定義②を使っています。鉄損計算のパネルのなかに”異常渦電流損失を分離する(FFT)”というチェックボックスがありますので、それをチェックすると、異常渦電流損失が分離、計算されます。(図63)
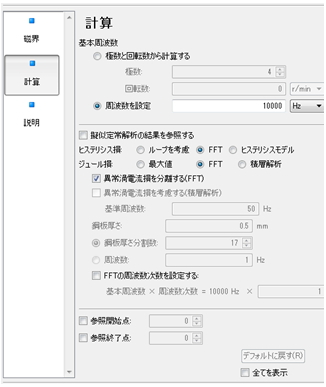図63 鉄損スタディのプロパティ設定アルゴリズム1、2で異常渦電流損を表示させるためには[異常渦電流損を分離する(FFT)]をチェックする。 図はアルゴリズム1での設定例。
ここで１つ注意をしておきたいのですが、この異常渦電流損失の分離、計算はあくまでも分離であることです。つまり、異常渦電流損失の分離の有無に関わらず、全鉄損量は変わりません。分離をしない場合でも異常渦電流損失は古典的渦電流損失に含まれていたわけです。ああ良かった。
では、アルゴリズム3は？当然の疑問です。実は上の3つの方法のいずれでもありません。というのは、思い出していただきたいのですが、アルゴリズム3の最大の特長は測定値に直接依存しておらず、渦電流損失について言えば、測定の周波数上限の影響を受けないことでした。一方、上の異常渦電流損失は、いずれも、測定値から導き出されています。これはアルゴリズム3にとっては困ります。
そこで、補正係数\(κ\)というものを導入しアルゴリズム3で計算された古典的渦電流損失に乗じ、これで異常渦電流損失の効果を取り込みます<49>。式で書くと次のようになります。
\(P_{ec} + P_{ex} = kP_{ec} \quad \cdots \) (19)
補正係数\(k\)は、表皮効果を無視した古典的渦電流損失\(P_{en}\)と表皮効果が無視できる周波数における測定値\(P_{em}\)の比から次のように求めます。
\( k = \frac{p^m_e}{p^n_e} \quad \cdots \) (20)
ここで、鉄損特性を使っていますが、これは低周波の特性を使うだけですので、利用時の周波数上限には影響しないことを注意しておきたいと思います。この方法も他の方法同様、完璧なわけではありません。周波数依存性など気になるところはあり、手法の改良も進められています<50>。
JMAGでこの計算を行うためには、鉄損計算のパネルにてジュール損を「積層解析」に指定し、「異常渦電流損を考慮する(積層解析)」をチェックします。アルゴリズム3の渦電流損失の計算は電気抵抗率しか必要としませんでしたが、上の説明の通り、補正係数\(k\)をだすために鉄損特性が必要になります。
では異常渦電流損失を含めて第9話で行ったリングコアの損失計算をやってみましょう。条件は同じです。結果を図64に示します。どうでしょうか？
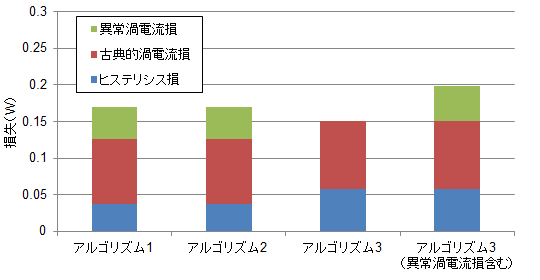図64 直流成分を加えた正弦波電流を印加した時の損失計算比較第9話 図34のアルゴリズム3に異常渦電流損を考慮して計算(直流成分0A、周波数1kHz)
アルゴリズム1、2については異常渦電流損と古典的渦電流損を分割。
第9話 図34でのアルゴリズム1,2とアルゴリズム3の渦電流損の違いは
アルゴリズム3で異常渦電流損が含まれていなかったことで説明できる。
[*1] 切断された単板は幅が30mmになるように並べて測定を実施
